
【題目】已知橢圓![]() 的兩個焦點為
的兩個焦點為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 是橢圓
是橢圓![]() 的右頂點,過點
的右頂點,過點![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,直線
兩點,直線![]() ,
, ![]() 與直線
與直線![]() 分別交于
分別交于![]() ,
, ![]() 兩點.求證:點
兩點.求證:點![]() 在以
在以![]() 為直徑的圓上.
為直徑的圓上.
【答案】(1)![]() ;(2)見解析
;(2)見解析
【解析】試題分析:(1)由題意,設橢圓方程為![]() ,
,
則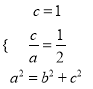 ,解出
,解出![]() ,即可得到橢圓
,即可得到橢圓![]() 的方程;
的方程;
( 2)由(1)可得![]() . 考慮直線
. 考慮直線![]() 不存在斜率時,可得
不存在斜率時,可得![]() .
.![]() 在以
在以![]() 為直徑的圓上. 當直線
為直徑的圓上. 當直線![]() 存在斜率時,設
存在斜率時,設![]() 方程為
方程為![]() ,
, ![]() 、
、![]() .
.
由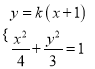 可得
可得![]() . 直線
. 直線![]() 方程為
方程為![]() ,得
,得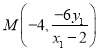 , 同理,
, 同理, 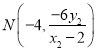 . 求出
. 求出![]() ,可證
,可證![]() .即
.即![]() 在以
在以![]() 為直徑的圓上.
為直徑的圓上.
試題解析:
(1)由題意,設橢圓方程為![]() ,
,
則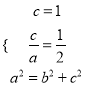
得![]()
所以橢圓方程為![]()
(2)證明:由(Ⅰ)可得![]() .
.
當直線![]() 不存在斜率時,可得
不存在斜率時,可得![]()
直線![]() 方程為
方程為![]() ,令
,令![]() 得
得![]() ,
,
同理,得![]() .
.
所以![]() ,
,
得![]() .
.
所以![]() ,
,![]() 在以
在以![]() 為直徑的圓上.
為直徑的圓上.
當直線![]() 存在斜率時,設
存在斜率時,設![]() 方程為
方程為![]() ,
, ![]() 、
、![]() .
.
由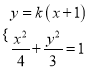 可得
可得![]() .
.
顯然![]() ,
,![]() ,
,
直線![]() 方程為
方程為![]() ,得
,得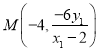 ,
,
同理, 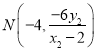 .
.
所以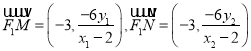 .
.
![]()
因為![]()
所以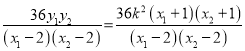

所以![]()
所以![]() ,
, ![]() 在以
在以![]() 為直徑的圓上.
為直徑的圓上.
綜上, ![]() 在以
在以![]() 為直徑的圓上.
為直徑的圓上.


科目:高中數學 來源: 題型:
【題目】若數列{![]() }的前n項和Sn=2
}的前n項和Sn=2![]() -2.
-2.
(1)求數列{![]() }的通項公式;
}的通項公式;
(2)若bn=![]() log
log![]()
![]() ,Sn=b1+b2+…+bn,對任意正整數n,Sn+(n+m)
,Sn=b1+b2+…+bn,對任意正整數n,Sn+(n+m)![]() <0恒成立,試求實數m的取值范圍.
<0恒成立,試求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線![]() 的焦點為
的焦點為![]() ,過點
,過點![]() 的直線與拋物線相交于
的直線與拋物線相交于![]() 兩點,與拋物線的準線相交于點
兩點,與拋物線的準線相交于點![]() ,
, ![]() ,則
,則![]() 與
與![]() 的面積之比
的面積之比![]() __________.
__________.
【答案】![]()
【解析】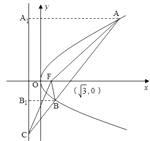
由題意可得拋物線的焦點![]() 的坐標為
的坐標為![]() ,準線方程為
,準線方程為![]() 。
。
如圖,設![]() ,過A,B分別向拋物線的準線作垂線,垂足分別為E,N,則
,過A,B分別向拋物線的準線作垂線,垂足分別為E,N,則
![]() ,解得
,解得![]() 。
。
把![]() 代入拋物線
代入拋物線![]() ,解得
,解得![]() 。
。
∴直線AB經過點![]() 與點
與點![]() ,
,
故直線AB的方程為![]() ,代入拋物線方程解得
,代入拋物線方程解得![]() 。
。
∴![]() 。
。
在![]() 中,
中, ![]() ,
,
∴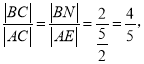
∴![]() 。答案:
。答案: ![]()
點睛:
在解決與拋物線有關的問題時,要注意拋物線的定義在解題中的應用。拋物線定義有兩種用途:一是當已知曲線是拋物線時,拋物線上的點M滿足定義,它到準線的距離為d,則|MF|=d,可解決有關距離、最值、弦長等問題;二是利用動點滿足的幾何條件符合拋物線的定義,從而得到動點的軌跡是拋物線.
【題型】填空題
【結束】
17
【題目】已知![]() 三個內角
三個內角![]() 所對的邊分別是
所對的邊分別是![]() ,若
,若![]() .
.
(1)求角![]() ;
;
(2)若![]() 的外接圓半徑為2,求
的外接圓半徑為2,求![]() 周長的最大值.
周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
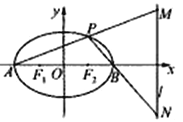
【題目】橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,若橢圓過點
,若橢圓過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 為橢圓的左、右頂點,
為橢圓的左、右頂點, ![]() (
(![]() )為橢圓上一動點,設直線
)為橢圓上一動點,設直線![]() 分別交直線
分別交直線![]() :
: ![]() 于點
于點![]() ,判斷線段
,判斷線段![]() 為直徑的圓是否經過定點,若是,求出該定點坐標;若不恒過定點,說明理由.
為直徑的圓是否經過定點,若是,求出該定點坐標;若不恒過定點,說明理由.
【答案】(1) ![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】試題分析:(1)將點坐標代人橢圓方程 并與離心率聯立方程組,解得![]() ,
, ![]() (2)根據點斜式得直線
(2)根據點斜式得直線![]() 方程,與直線
方程,與直線![]() 聯立解得點
聯立解得點![]() 坐標,根據向量關系得
坐標,根據向量關系得![]() 為直徑的圓方程,最后代人橢圓方程進行化簡,并根據恒等式成立條件求定點坐標.
為直徑的圓方程,最后代人橢圓方程進行化簡,并根據恒等式成立條件求定點坐標.
試題解析:(1)由已知![]() ,
,
∴![]() ①
①
∵橢圓過點![]() ,
,
∴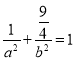 ②
②
聯立①②得![]() ,
, ![]()
∴橢圓方程為![]()
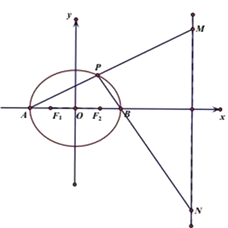
(2)設![]() ,已知
,已知![]()
∵![]() ,∴
,∴![]()
∴![]() 都有斜率
都有斜率
∴![]()
∴![]() ③
③
∵![]()
∴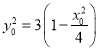 ④
④
將④代入③得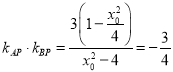
設![]() 方程
方程![]()
∴![]() 方程
方程![]()
∴![]()
由對稱性可知,若存在定點,則該定點必在![]() 軸上,設該定點為
軸上,設該定點為![]()
則![]()
∴![]()
∴![]() ,∴
,∴![]()
∴存在定點![]() 或
或![]() 以線段
以線段![]() 為直徑的圓恒過該定點.
為直徑的圓恒過該定點.
點睛:定點的探索與證明問題
(1)探索直線過定點時,可設出直線方程為![]() ,然后利用條件建立
,然后利用條件建立![]() 等量關系進行消元,借助于直線系的思想找出定點.
等量關系進行消元,借助于直線系的思想找出定點.
(2)從特殊情況入手,先探求定點,再證明與變量無關.
【題型】解答題
【結束】
21
【題目】已知函數![]() ,曲線
,曲線![]() 在
在![]() 處的切線經過點
處的切線經過點![]() .
.
(1)證明: ![]() ;
;
(2)若當![]() 時,
時, 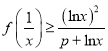 ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為積極響應國家“陽光體育運動”的號召,某學校在了解到學生的實際運動情況后,發起以“走出教室,走到操場,走到陽光”為口號的課外活動倡議。為調查該校學生每周平均體育運動時間的情況,從高一高二基礎年級與高三三個年級學生中按照4:3:3的比例分層抽樣,收集300位學生每周平均體育運動時間的樣本數據(單位:小時),得到如圖所示的頻率分布直方圖。

(1)據圖估計該校學生每周平均體育運動時間.并估計高一年級每周平均體育運動時間不足4小時的人數;
(2)規定每周平均體育運動時間不少于6小時記為“優秀”,否則為“非優秀”,在樣本數據中,有30位高三學生的每周平均體育運動時間不少于6小時,請完成下列![]() 列聯表,并判斷是否有99%的把握認為“該校學生的每周平均體育運動時間是否“優秀”與年級有關”.
列聯表,并判斷是否有99%的把握認為“該校學生的每周平均體育運動時間是否“優秀”與年級有關”.
基礎年級 | 高三 | 合計 | |
優秀 | |||
非優秀 | |||
合計 | 300 |
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附:K2![]() ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC-A1B1C1中,已知AA1⊥底面ABC,AC⊥BC,四邊形BB1C1C為正方形,設AB1的中點為D,B1C∩BC1=E.
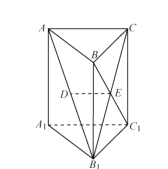
求證:(1)DE∥平面AA1C1C;
(2)BC1⊥平面AB1C.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩班舉行電腦漢字錄入比賽,參賽學生每分鐘錄入漢字的個數經統計計算后填入下表,某同學根據表中數據分析得出的結論正確的是( )
班級 | 參加人數 | 中位數 | 方差 | 平均數 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
A.甲、乙兩班學生成績的平均數相同
B.甲班的成績波動比乙班的成績波動大
C.乙班優秀的人數多于甲班優秀的人數(每分鐘輸入漢字數≥150個為優秀)
D.甲班成績的眾數小于乙班成績的眾數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:極坐標與參數方程
在平面直角坐標系![]() 中,將曲線
中,將曲線![]() (
(![]() 為參數) 上任意一點
為參數) 上任意一點![]() 經過伸縮變換
經過伸縮變換 后得到曲線
后得到曲線![]() 的圖形.以坐標原點
的圖形.以坐標原點![]() 為極點,x軸的非負半軸為極軸,取相同的單位長度建立極坐標系,已知直線
為極點,x軸的非負半軸為極軸,取相同的單位長度建立極坐標系,已知直線![]() .
.
(Ⅰ)求曲線![]() 和直線
和直線![]() 的普通方程;
的普通方程;
(Ⅱ)點P為曲線![]() 上的任意一點,求點P到直線
上的任意一點,求點P到直線![]() 的距離的最大值及取得最大值時點P的坐標.
的距離的最大值及取得最大值時點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com