
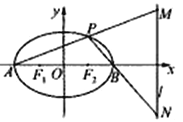
【題目】橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,若橢圓過點
,若橢圓過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 為橢圓的左、右頂點,
為橢圓的左、右頂點, ![]() (
(![]() )為橢圓上一動點,設直線
)為橢圓上一動點,設直線![]() 分別交直線
分別交直線![]() :
: ![]() 于點
于點![]() ,判斷線段
,判斷線段![]() 為直徑的圓是否經過定點,若是,求出該定點坐標;若不恒過定點,說明理由.
為直徑的圓是否經過定點,若是,求出該定點坐標;若不恒過定點,說明理由.
【答案】(1) ![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】試題分析:(1)將點坐標代人橢圓方程 并與離心率聯立方程組,解得![]() ,
, ![]() (2)根據點斜式得直線
(2)根據點斜式得直線![]() 方程,與直線
方程,與直線![]() 聯立解得點
聯立解得點![]() 坐標,根據向量關系得
坐標,根據向量關系得![]() 為直徑的圓方程,最后代人橢圓方程進行化簡,并根據恒等式成立條件求定點坐標.
為直徑的圓方程,最后代人橢圓方程進行化簡,并根據恒等式成立條件求定點坐標.
試題解析:(1)由已知![]() ,
,
∴![]() ①
①
∵橢圓過點![]() ,
,
∴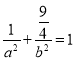 ②
②
聯立①②得![]() ,
, ![]()
∴橢圓方程為![]()
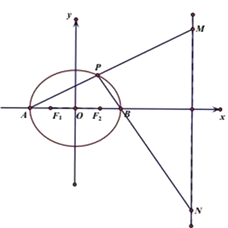
(2)設![]() ,已知
,已知![]()
∵![]() ,∴
,∴![]()
∴![]() 都有斜率
都有斜率
∴![]()
∴![]() ③
③
∵![]()
∴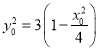 ④
④
將④代入③得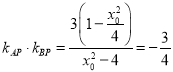
設![]() 方程
方程![]()
∴![]() 方程
方程![]()
∴![]()
由對稱性可知,若存在定點,則該定點必在![]() 軸上,設該定點為
軸上,設該定點為![]()
則![]()
∴![]()
∴![]() ,∴
,∴![]()
∴存在定點![]() 或
或![]() 以線段
以線段![]() 為直徑的圓恒過該定點.
為直徑的圓恒過該定點.
點睛:定點的探索與證明問題
(1)探索直線過定點時,可設出直線方程為![]() ,然后利用條件建立
,然后利用條件建立![]() 等量關系進行消元,借助于直線系的思想找出定點.
等量關系進行消元,借助于直線系的思想找出定點.
(2)從特殊情況入手,先探求定點,再證明與變量無關.
【題型】解答題
【結束】
21
【題目】已知函數![]() ,曲線
,曲線![]() 在
在![]() 處的切線經過點
處的切線經過點![]() .
.
(1)證明: ![]() ;
;
(2)若當![]() 時,
時, 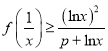 ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)證明見解析;(2) ![]() .
.
【解析】試題分析:(1)先根據導數幾何意義得切線斜率為![]() ,再根據切線過點
,再根據切線過點![]() ,解得
,解得![]() 導數可得導函數零點,列表分析導函數符號變號規律可得函數單調性,根據函數單調性可得函數最小值為0,即得結論,(2)先化簡不等式為
導數可得導函數零點,列表分析導函數符號變號規律可得函數單調性,根據函數單調性可得函數最小值為0,即得結論,(2)先化簡不等式為![]() ,分離得
,分離得![]() ,再利用導數求函數
,再利用導數求函數![]() 單調性,利用羅伯特法則求最大值,即得
單調性,利用羅伯特法則求最大值,即得![]() 的取值范圍.
的取值范圍.
試題解析:(1)曲線![]() 在
在![]() 處的切線為
處的切線為![]() ,即
,即![]()
由題意得![]() ,解得
,解得![]()
所以![]()
從而![]()
因為當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() .
.
所以![]() 在區間
在區間![]() 上是減函數,區間
上是減函數,區間![]() 上是增函數,
上是增函數,
從而![]() .
.
(2)由題意知,當![]() 時,
時, ![]() ,所以
,所以![]()
從而當![]() 時,
時, ![]() ,
,
由題意知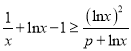 ,即
,即![]() ,其中
,其中![]()
設![]() ,其中
,其中![]()
設![]() ,即
,即![]() ,其中
,其中![]()
則![]() ,其中
,其中![]()
(1)當![]() 時,因為
時,因為![]() 時,
時, ![]() ,所以
,所以![]() 是增函數
是增函數
從而當![]() 時,
時, ![]() ,
,
所以![]() 是增函數,從而
是增函數,從而![]() .
.
故當![]() 時符合題意.
時符合題意.
(2)當![]() 時,因為
時,因為![]() 時,
時, ![]() ,
,
所以![]() 在區間
在區間![]() 上是減函數
上是減函數
從而當![]() 時,
時, ![]()
所以![]() 在
在![]() 上是減函數,從而
上是減函數,從而![]()
故當![]() 時不符合題意.
時不符合題意.
(3)當![]() 時,因為
時,因為![]() 時,
時, ![]() ,所以
,所以![]() 是減函數
是減函數
從而當![]() 時,
時, ![]()
所以![]() 是減函數,從而
是減函數,從而![]()
故當![]() 時不符合題意
時不符合題意
綜上![]() 的取值范圍是
的取值范圍是![]() .
.


 一線名師提優試卷系列答案
一線名師提優試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:高中數學 來源: 題型:
【題目】中國古代數學家劉徽在《九章算術注》中,稱一個正方體內兩個互相垂直的內切圓柱所圍成的立體為“牟合方蓋”,如圖(1)(2),劉徽未能求得牟合方蓋的體積,直言“欲陋形措意,懼失正理”,不得不說“敢不闕疑,以俟能言者”.約200年后,祖沖之的兒子祖暅提出“冪勢既同,則積不容異”,后世稱為祖暅原理,即:兩等高立體,若在每一等高處的截面積都相等,則兩立體體積相等.如圖(3)(4),祖暅利用八分之一正方體去掉八分之一牟合方蓋后的幾何體與長寬高皆為八分之一正方體的邊長的倒四棱錐“等冪等積”,計算出牟合方蓋的體積,據此可知,牟合方蓋的體積與其外切正方體的體積之比為( )
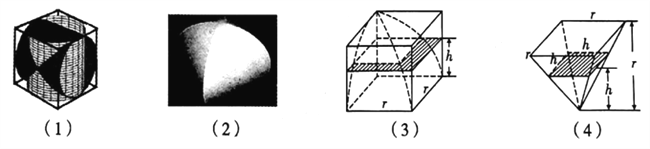
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經調查,3個成年人中就有一個高血壓,那么什么是高血壓?血壓多少是正常的?經國際衛生組織對大量不同年齡的人群進行血壓調查,得出隨年齡變化,收縮壓的正常值變化情況如下表:

其中:  ,
, ![]() ,
, ![]()
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;(
;(![]() 的值精確到0.01)
的值精確到0.01)
(3)若規定,一個人的收縮壓為標準值的0.9~1.06倍,則為血壓正常人群;收縮壓為標準值的1.06~1.12倍,則為輕度高血壓人群;收縮壓為標準值的1.12~1.20倍,則為中度高血壓人群;收縮壓為標準值的1.20倍及以上,則為高度高血壓人群.一位收縮壓為180mmHg的70歲的老人,屬于哪類人群?
【答案】(1)答案見解析;(2) ![]() ;(3)中度高血壓人群.
;(3)中度高血壓人群.
【解析】試題分析:(1)將數據對應描點,即得散點圖,(2)先求均值,再代人公式求![]() ,利用
,利用![]() 求
求![]() ,(3)根據回歸直線方程求自變量為180時對應函數值,再求與標準值的倍數,確定所屬人群.
,(3)根據回歸直線方程求自變量為180時對應函數值,再求與標準值的倍數,確定所屬人群.
試題解析:(1) 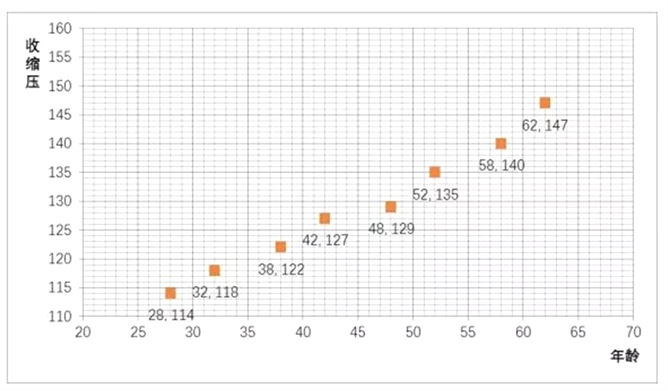
(2)![]()
![]()
∴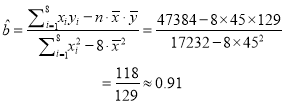
![]()
∴回歸直線方程為![]() .
.
(3)根據回歸直線方程的預測,年齡為70歲的老人標準收縮壓約為![]() (mmHg)∵
(mmHg)∵![]()
∴收縮壓為180mmHg的70歲老人為中度高血壓人群.
【題型】解答題
【結束】
19
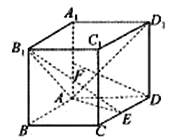
【題目】如圖,四棱柱![]() 的底面為菱形,
的底面為菱形, ![]() ,
, ![]() ,
, ![]() 為
為![]() 中點.
中點.
(1)求證: ![]() 平面
平面![]() ;
;
(2)若![]() 底面
底面![]() ,且直線
,且直線![]() 與平面
與平面![]() 所成線面角的正弦值為
所成線面角的正弦值為![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點為
的兩個焦點為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 是橢圓
是橢圓![]() 的右頂點,過點
的右頂點,過點![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,直線
兩點,直線![]() ,
, ![]() 與直線
與直線![]() 分別交于
分別交于![]() ,
, ![]() 兩點.求證:點
兩點.求證:點![]() 在以
在以![]() 為直徑的圓上.
為直徑的圓上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() ,
,![]() ,函數
,函數![]() .
.
(1)求![]() 的最小正周期及
的最小正周期及![]() 圖象的對稱軸方程;
圖象的對稱軸方程;
(2)若先將![]() 的圖象上每個點縱坐標不變,橫坐標變為原來的2倍,然后再向左平移
的圖象上每個點縱坐標不變,橫坐標變為原來的2倍,然后再向左平移![]() 個單位長度得到函數
個單位長度得到函數![]() 的圖象,求函數
的圖象,求函數![]() 在區間
在區間![]() 內的所有零點之和.
內的所有零點之和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com