
【題目】已知向量![]() ,
,![]() ,函數
,函數![]() .
.
(1)求![]() 的最小正周期及
的最小正周期及![]() 圖象的對稱軸方程;
圖象的對稱軸方程;
(2)若先將![]() 的圖象上每個點縱坐標不變,橫坐標變為原來的2倍,然后再向左平移
的圖象上每個點縱坐標不變,橫坐標變為原來的2倍,然后再向左平移![]() 個單位長度得到函數
個單位長度得到函數![]() 的圖象,求函數
的圖象,求函數![]() 在區間
在區間![]() 內的所有零點之和.
內的所有零點之和.
 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案科目:高中數學 來源: 題型:
【題目】已知![]() 是公差不為零的等差數列,滿足
是公差不為零的等差數列,滿足![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比數列.
成等比數列.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設數列![]() 滿足
滿足![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)設等差數列![]() 的公差為
的公差為![]() ,由a3=7,且
,由a3=7,且![]() 、
、![]() 、
、![]() 成等比數列.可得
成等比數列.可得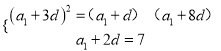 ,解之得即可得出數列
,解之得即可得出數列![]() 的通項公式;
的通項公式;
2)由(1)得![]() ,則
,則![]() ,由裂項相消法可求數列
,由裂項相消法可求數列![]() 的前
的前![]() 項和
項和![]() .
.
試題解析:(1)設數列![]() 的公差為
的公差為![]() ,且
,且![]() 由題意得
由題意得![]() ,
,
即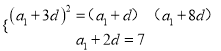 ,解得
,解得![]() ,
,
所以數列![]() 的通項公式
的通項公式![]() .
.
(2)由(1)得![]()
![]() ,
,
![]()
![]() .
.
【題型】解答題
【結束】
18
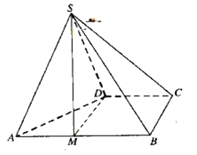
【題目】四棱錐![]() 的底面
的底面![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 為正三角形.
為正三角形.
(1)點![]() 為棱
為棱![]() 上一點,若
上一點,若![]() 平面
平面![]() ,
,![]() ,求實數
,求實數![]() 的值;
的值;
(2)求點B到平面SAD的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是兩條不同的直線,
是兩條不同的直線, ![]() 是兩個不同的平面,則下列命題中正確的是( )
是兩個不同的平面,則下列命題中正確的是( )
A. 若![]() ,
, ![]() ,則
,則![]()
B. 若![]() ,
, ![]() ,則
,則![]()
C. 若![]() ,
, ![]() ,
, ![]() ,則
,則![]()
D. 若![]() ,且
,且![]() ,點
,點![]() ,直線
,直線![]() ,則
,則![]()
【答案】C
【解析】A. 若![]() ,
, ![]() ,則
,則![]() 或
或![]() ;
;
B. 若![]() ,
, ![]() ,則
,則![]() 無交點,即平行或異面;
無交點,即平行或異面;
C. 若![]() ,
, ![]() ,
, ![]() ,過
,過![]() 作平面與
作平面與![]() 分別交于直線s,t,則
分別交于直線s,t,則![]() ,
, ![]() ,所以
,所以![]() t,再根據線面平行判定定理得
t,再根據線面平行判定定理得![]() ,因為
,因為![]() ,
, ![]() ,所以
,所以![]() ,即
,即![]()
D. 若![]() ,且
,且![]() ,點
,點![]() ,直線
,直線![]() ,當B在平面
,當B在平面![]() 內時才有
內時才有![]() ,
,
綜上選C.
【題型】單選題
【結束】
11
【題目】甲、乙、丙、丁四位同學參加比賽,只有其中三位獲獎.甲說:“乙或丙未獲獎”;乙說:“甲、丙都獲獎”;丙說:“我未獲獎”;丁說:“乙獲獎”.四位同學的話恰有兩句是對的,則( )
A. 甲和乙不可能同時獲獎 B. 丙和丁不可能同時獲獎
C. 乙和丁不可能同時獲獎 D. 丁和甲不可能同時獲獎
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,若橢圓過點
,若橢圓過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
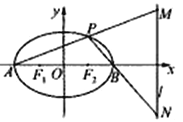
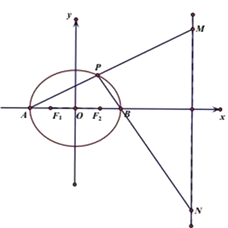
(2)若![]() 為橢圓的左、右頂點,
為橢圓的左、右頂點, ![]() (
(![]() )為橢圓上一動點,設直線
)為橢圓上一動點,設直線![]() 分別交直線
分別交直線![]() :
: ![]() 于點
于點![]() ,判斷線段
,判斷線段![]() 為直徑的圓是否經過定點,若是,求出該定點坐標;若不恒過定點,說明理由.
為直徑的圓是否經過定點,若是,求出該定點坐標;若不恒過定點,說明理由.
【答案】(1) ![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】試題分析:(1)將點坐標代人橢圓方程 并與離心率聯立方程組,解得![]() ,
, ![]() (2)根據點斜式得直線
(2)根據點斜式得直線![]() 方程,與直線
方程,與直線![]() 聯立解得點
聯立解得點![]() 坐標,根據向量關系得
坐標,根據向量關系得![]() 為直徑的圓方程,最后代人橢圓方程進行化簡,并根據恒等式成立條件求定點坐標.
為直徑的圓方程,最后代人橢圓方程進行化簡,并根據恒等式成立條件求定點坐標.
試題解析:(1)由已知![]() ,
,
∴![]() ①
①
∵橢圓過點![]() ,
,
∴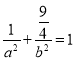 ②
②
聯立①②得![]() ,
, ![]()
∴橢圓方程為![]()
(2)設![]() ,已知
,已知![]()
∵![]() ,∴
,∴![]()
∴![]() 都有斜率
都有斜率
∴![]()
∴![]() ③
③
∵![]()
∴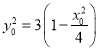 ④
④
將④代入③得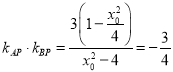
設![]() 方程
方程![]()
∴![]() 方程
方程![]()
∴![]()
由對稱性可知,若存在定點,則該定點必在![]() 軸上,設該定點為
軸上,設該定點為![]()
則![]()
∴![]()
∴![]() ,∴
,∴![]()
∴存在定點![]() 或
或![]() 以線段
以線段![]() 為直徑的圓恒過該定點.
為直徑的圓恒過該定點.
點睛:定點的探索與證明問題
(1)探索直線過定點時,可設出直線方程為![]() ,然后利用條件建立
,然后利用條件建立![]() 等量關系進行消元,借助于直線系的思想找出定點.
等量關系進行消元,借助于直線系的思想找出定點.
(2)從特殊情況入手,先探求定點,再證明與變量無關.
【題型】解答題
【結束】
21
【題目】已知函數![]() ,曲線
,曲線![]() 在
在![]() 處的切線經過點
處的切線經過點![]() .
.
(1)證明: ![]() ;
;
(2)若當![]() 時,
時, 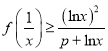 ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以橢圓
,以橢圓![]() 的任意三個頂點為頂點的三角形的面積是
的任意三個頂點為頂點的三角形的面積是![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 是橢圓
是橢圓![]() 的右頂點,點
的右頂點,點![]() 在
在![]() 軸上.若橢圓
軸上.若橢圓![]() 上存在點
上存在點![]() ,使得
,使得![]() ,求點
,求點![]() 橫坐標的取值范圍.
橫坐標的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC-A1B1C1中,已知AA1⊥底面ABC,AC⊥BC,四邊形BB1C1C為正方形,設AB1的中點為D,B1C∩BC1=E.
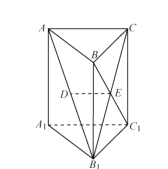
求證:(1)DE∥平面AA1C1C;
(2)BC1⊥平面AB1C.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是某省從1月21日至2月24日的新冠肺炎每日新增確診病例變化曲線圖.

若該省從1月21日至2月24日的新冠肺炎每日新增確診人數按日期順序排列構成數列![]() ,
,![]() 的前n項和為
的前n項和為![]() ,則下列說法中正確的是( )
,則下列說法中正確的是( )
A.數列![]() 是遞增數列B.數列
是遞增數列B.數列![]() 是遞增數列
是遞增數列
C.數列![]() 的最大項是
的最大項是![]() D.數列
D.數列![]() 的最大項是
的最大項是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據拋物線的光學原理:平行于拋物線的軸的光線,經拋物線反射后,反射光線必經過焦點.然后求解此題:有一條光線沿直線![]() 射到拋物線
射到拋物線![]() (
(![]() )上的一點
)上的一點![]() ,經拋物線反射后,反射光線所在直線的斜率為
,經拋物線反射后,反射光線所在直線的斜率為![]() .
.
(Ⅰ)求拋物線的標準方程;
(Ⅱ)過定點![]() 的直線l與拋物線交于
的直線l與拋物線交于![]() 兩點,與直線
兩點,與直線![]() 交于Q點,若
交于Q點,若![]() ,
,![]() =
=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga(x+1),g(x)=2loga(2x+t)(t∈R),其中x∈[0,15],a>0,且a≠1.
(1)若1是關于x的方程f(x)﹣g(x)=0的一個解,求t的值;
(2)當0<a<1時,不等式f(x)≥g(x)恒成立,求t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com