
分析 (Ⅰ)設等差數列{log2(an+1)}的公差為d.由a1=1,a3=7可求d,由等差數列的通項公式可求log2(an+1),進而可求an;
(Ⅱ)利用(Ⅰ)中的通項公式和分組求和法進行解答即可.
解答 解:(Ⅰ)設等差數列{log2(an+1)}的公差為d.
由a1=1,a3=7得log28=log22+2d,即d=1.
所以log2(an+1)=1+(n-1)×1=n,
即${a_n}+1={2^n}$,
∴${a_n}={2^n}-1$.
(Ⅱ)Sn=a1+a2+a3+…+an=(21-1)+(22-1)+(23-1)+…+(2n-1)=21+22+23+…+2n-n=$\frac{{2(1-{2^n})}}{1-2}-n$=2n+1-2-n.
點評 本題主要考查數列通項公式和前n項和的求解,利用分組求和法是解決本題的關鍵.


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
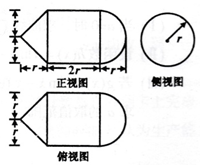
| A. | 4π | B. | 2π | C. | $\frac{11}{3}$π | D. | 3π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a≤-1 | B. | a≥-1 | C. | a≤1 | D. | a≥1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {2,6,8} | B. | {2,4,6,8} | C. | {0,2,4,6,8} | D. | {0,2,6,8} |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com