
 已知一個由11人組成的評審委員會以投票方式從符合要求的甲,乙兩名候選人中選出一人參加一次活動.投票要求委員會每人只能選一人且不能棄選,每位委員投票不受他人影響.投票結果由一人唱票,一人統(tǒng)計投票結果.
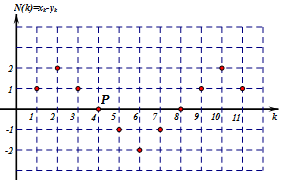
已知一個由11人組成的評審委員會以投票方式從符合要求的甲,乙兩名候選人中選出一人參加一次活動.投票要求委員會每人只能選一人且不能棄選,每位委員投票不受他人影響.投票結果由一人唱票,一人統(tǒng)計投票結果.分析 (Ⅰ)因縱軸表示每次唱票時甲的得票數(shù)減乙的得票數(shù),故從圖表可看出,唱票順序為甲,甲,乙,乙,乙,乙,甲,甲,甲,甲,乙,由此能求出結果.
(Ⅱ) 若事件A“候選人甲比乙恰多3票勝出”發(fā)生,由甲乙得票共11張,故甲得7票,乙得4票,由每位委員投票不受他人影響,且每人投甲的概率為$\frac{1}{2}$,能求出事件A發(fā)生的概率.
(Ⅲ)設事件B為“在已知條件下,在唱票過程中出現(xiàn)甲乙兩人得票數(shù)相同情況”,根據(jù)第一問的分析可知,如果只知道選舉結果,則在生成這種結果的過程中存在兩人選票一樣的可能.由第一問提供的圖表可看出,由于結果中甲的得票數(shù)為7高于乙的得票數(shù)4,故當?shù)谝粡堖x票為乙時,散點圖中一定存在點在橫軸上,由此能求出事件B的概率.
解答 解:(Ⅰ)因縱軸表示每次唱票時甲的得票數(shù)減乙的得票數(shù)
故從圖表可看出,唱票順序為甲,甲,乙,乙,乙,乙,甲,甲,甲,甲,乙
故甲勝出(本結論可由第11個點的位置馬上就可判斷甲贏,如果最后一個點在橫軸下,則乙贏),
y7=4(從圖上看第7個點在上升段,應是甲得一票,而之前的下降段,從第二點算起共4個點,故都是乙得票)
圖中點P從位置上看意味著x4-y4=0,即甲乙第4輪唱票后得票數(shù)相同.(答案為各得2票也正確).
(Ⅱ) 若事件A“候選人甲比乙恰多3票勝出”發(fā)生,
由甲乙得票共11張,故甲得7票,乙得4票,
因每位委員投票不受他人影響,且每人投甲的概率為$\frac{1}{2}$,
故事件A發(fā)生的概率$p(A)=C_{11}^4{(\frac{1}{2})^7}{(\frac{1}{2})^4}=\frac{165}{1024}$.
(Ⅲ)設事件B為“在已知條件下,在唱票過程中出現(xiàn)甲乙兩人得票數(shù)相同情況”,
根據(jù)第一問的分析可知,如果只知道選舉結果,則在生成這種結果的過程中存在兩人選票一樣的可能.
由第一問提供的圖表可看出,由于結果中甲的得票數(shù)為7高于乙的得票數(shù)4,
故當?shù)谝粡堖x票為乙時,散點圖中一定存在點在橫軸上,
即出現(xiàn)兩人得票相等的情況,這樣的點圖一共有$C_{11-1}^{4-1}=C_{10}^3$種(即10位評委里再選3位投給乙)
當?shù)谝粡堖x票為甲時,散點圖可能有點在橫軸上,也可能無點在橫軸上,如下圖所示的兩種投票可能: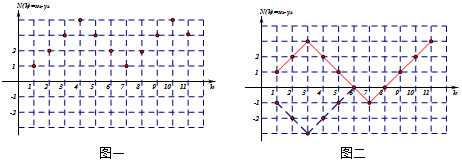
而圖二的每一種情況對于第一張選票為乙時的情況一一對應,(最后一次票數(shù)相等前圖形關于橫軸對稱,最后一次票數(shù)相等后圖形重合)
故當?shù)谝粡堖x票為甲時出現(xiàn)兩人得票相等情況的點圖同樣為$C_{10}^3$種
而所有與唱票情況對應的散點圖共$C_{11}^4$種
故事件B的概率為$p(B)=\frac{{2C_{10}^3}}{{C_{11}^4}}=\frac{8}{11}$.
點評 本題考查概率的求法及應用,涉及到n次獨立重復試驗中事件A恰好發(fā)生k次的概率的計算公式、排列組合等基礎知識,考查函數(shù)與方程思想、數(shù)形結合思想,是中檔題.


科目:高中數(shù)學 來源: 題型:選擇題
| A. | $\frac{{27\sqrt{3}}}{4}$ | B. | 9 | C. | $\frac{81}{4}$ | D. | $\frac{27}{4}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | 充分必要條件 | B. | 充分不必要條件 | ||
| C. | 必要不充分條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com