
分析 (1)由題意可知:當(dāng)n=1時,a1=1.當(dāng)n≥2時,a1+2a2+…+nan=4-$\frac{n+2}{{2}^{n-1}}$,a1+2a2+…+(n-1)an-1=4-$\frac{n+1}{{2}^{n-2}}$,兩式相減即可求得數(shù)列{an}的通項公式;
(2)由bn=(3n-2)$\frac{1}{{2}^{n-1}}$,采用“錯位相減法”即可求得數(shù)列{bn}的前n項和Sn.
解答 解:(1)當(dāng)n=1時,a1=4-$\frac{3}{{2}^{0}}$=1.
當(dāng)n≥2時,a1+2a2+…+nan=4-$\frac{n+2}{{2}^{n-1}}$…①
a1+2a2+…+(n-1)an-1=4-$\frac{n+1}{{2}^{n-2}}$…②
①-②得:nan=$\frac{n+1}{{2}^{n-2}}$-$\frac{n+2}{{2}^{n-1}}$=$\frac{1}{{2}^{n-1}}$(2n+2-n-2)=$\frac{n}{{2}^{n-1}}$
∴an=$\frac{1}{{2}^{n-1}}$,
當(dāng)n=1時,a1也適合上式,
∴數(shù)列{an}的通項公式an=$\frac{1}{{2}^{n-1}}$ (n∈N*).
(2)bn=(3n-2)$\frac{1}{{2}^{n-1}}$,
Sn=$\frac{1}{{2}^{0}}$+$\frac{4}{{2}^{1}}$+$\frac{7}{{2}^{2}}$+…+(3n-5)$\frac{1}{{2}^{n-2}}$+(3n-2)$\frac{1}{{2}^{n-1}}$,…①
$\frac{1}{2}$Sn=$\frac{1}{{2}^{1}}$+$\frac{4}{{2}^{2}}$+$\frac{7}{{2}^{3}}$+…+(3n-5)$\frac{1}{{2}^{n-1}}$+(3n-2)$\frac{1}{{2}^{n}}$,…②
①-②得:$\frac{1}{2}$Sn=1+3($\frac{1}{{2}^{1}}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n-1}}$ )-(3n-2)$\frac{1}{{2}^{n}}$
=1+3•$\frac{\frac{1}{2}-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-(3n-2)$\frac{1}{{2}^{n}}$=4-$\frac{3n+4}{{2}^{n}}$,
∴Sn=8-$\frac{3n+4}{{2}^{n-1}}$.
∴數(shù)列{bn}的前n項和Sn,Sn=8-$\frac{3n+4}{{2}^{n-1}}$.
點評 本題考查數(shù)列的遞推公式,等比數(shù)列前n項和公式,“錯位相減法”求數(shù)列的前n項和,考查計算能力,屬于中檔題.


科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | (2016,2017) | B. | (2016,2017] | C. | [2016,2017) | D. | (-2016,2017) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{7}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
| 年齡 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 頻數(shù) | 5 | 10 | 15 | 10 | 5 | 5 |
| 贊同 | 4 | 5 | 12 | 8 | 2 | 1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{5}{7}$ | B. | $\frac{6}{7}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
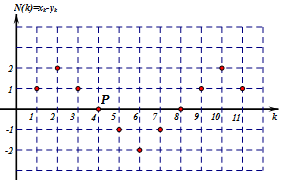 已知一個由11人組成的評審委員會以投票方式從符合要求的甲,乙兩名候選人中選出一人參加一次活動.投票要求委員會每人只能選一人且不能棄選,每位委員投票不受他人影響.投票結(jié)果由一人唱票,一人統(tǒng)計投票結(jié)果.
已知一個由11人組成的評審委員會以投票方式從符合要求的甲,乙兩名候選人中選出一人參加一次活動.投票要求委員會每人只能選一人且不能棄選,每位委員投票不受他人影響.投票結(jié)果由一人唱票,一人統(tǒng)計投票結(jié)果.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{2\sqrt{3}}{5}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com