
設函數
①當a=1時,求函數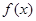 的極值;
的極值;
②若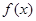 在
在 上是遞增函數,求實數a的取值范圍;
上是遞增函數,求實數a的取值范圍;
③當0<a<2時, ,求
,求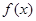 在該區間上的最小值.
在該區間上的最小值.
(1) ;(2)
;(2) ;(3)當x=2時取得最小值,為
;(3)當x=2時取得最小值,為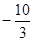 .
.
【解析】(1)求出導數 ,然后根據
,然后根據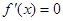 解出極值點,進而根據極值的確定方法求極值即可.
解出極值點,進而根據極值的確定方法求極值即可.
(2)由題意知把此問題轉化為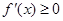 在
在 上恒成立問題解決即可,
上恒成立問題解決即可,
(3) 令 得,
得, ,由于0<a<2,所以當x=1或4時
,由于0<a<2,所以當x=1或4時 有可能取最大值,然后再分類討論可求出a值.再進一步確定最小值.
有可能取最大值,然后再分類討論可求出a值.再進一步確定最小值.
解:因為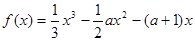
所以 …………………………………………1分
…………………………………………1分
① 因為a=1,所以
所以 …………………………………………2分
…………………………………………2分
令 得,
得, …………………………………………3分
…………………………………………3分
列表如下:
|
x |
|
-1 |
|
2 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
y |
增 |
極大值 |
減 |
極小值 |
增 |
當x=-1時取得極大值,為 ;
;
當x=2時取得極小值,為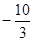 …………………………………………5分
…………………………………………5分
② 因為 在
在 上是遞增函數,
上是遞增函數,
所以 在
在 上恒成立,…………………………………………6分
上恒成立,…………………………………………6分
即 在
在 上恒成立.
上恒成立.

解得 …………………………………………8分
…………………………………………8分
③令 得,
得,
列表如下:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
y |
減 |
極小值 |
增 |
由上表知當x=1或4時 有可能取最大值,………………………………9分
有可能取最大值,………………………………9分
令 解得a=-4不符合題意舍.…………………………………………10分
解得a=-4不符合題意舍.…………………………………………10分
令 解得a=1…………………………………………11分
解得a=1…………………………………………11分
因為a=1,
所以
令 得,
得, …………………………………………12分
…………………………………………12分
列表如下:
|
x |
|
2 |
|
|
|
- |
0 |
+ |
|
y |
減 |
極小值 |
增 |
當x=2時取得最小值,為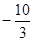 …………………………………………14分
…………………………………………14分


科目:高中數學 來源: 題型:
| 1 |
| 3 |
| a-1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| p+2e | x |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 4x2-7 | 2-x |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com