
【題目】已知函數![]() ,.
,.
(1)當![]() 為何值時,直線
為何值時,直線![]() 是曲線
是曲線![]() 的切線;
的切線;
(2)若不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】
(1)先令![]() ,求其導數,設切點為
,求其導數,設切點為![]() ,由直線
,由直線![]() 是曲線
是曲線![]() 的切線,得到
的切線,得到![]() ,用導數的方法研究函數
,用導數的方法研究函數![]() 的單調性,即可求出結果;
的單調性,即可求出結果;
(2)先令![]() ,對其求導,分別討論
,對其求導,分別討論![]() 和
和![]() 兩種情況,結合題意,即可得到結果.
兩種情況,結合題意,即可得到結果.
(1)令![]() ,
,![]() ,
,
設切點為![]() ,則
,則![]() ,
,![]() ,則
,則![]() .
.
令![]() ,
,![]() ,則函數
,則函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,且
上單調遞增,且![]() ,所以
,所以![]() .
.
(2)令![]() ,則
,則![]() ,
,
①當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,所以
,所以![]() 滿足題意.
滿足題意.
②當![]() 時,令
時,令![]() ,得
,得![]() ,
,
所以當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() .
.
所以函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(ⅰ)當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,所以
,所以![]() ,此時無解.
,此時無解.
(ⅱ)當![]() ,即
,即![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
所以![]() .
.
設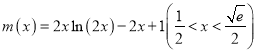 ,則
,則![]() ,
,
所以![]() 在
在 上單調遞增,
上單調遞增,
![]() ,不滿足題意.
,不滿足題意.
(ⅲ)當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,所以
,所以![]() 滿足題意.
滿足題意.
綜上所述:![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】某公司生產的某種產品,如果年返修率不超過千分之一,則其生產部門當年考核優秀,現獲得該公司2014-2018年的相關數據如下表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生產臺數 | 2 | 4 | 5 | 6 | 8 |
該產品的年利潤 | 30 | 40 | 60 | 50 | 70 |
年返修臺數(臺) | 19 | 58 | 45 | 71 | 70 |
注:![]()
(1)從該公司2014-2018年的相關數據中任意選取3年的數據,求這3年中至少有2年生產部門考核優秀的概率.
(2)利用上表中五年的數據求出年利潤![]() (百萬元)關于年生產臺數
(百萬元)關于年生產臺數![]() (萬臺)的回歸直線方程是
(萬臺)的回歸直線方程是![]() ①.現該公司計劃從2019年開始轉型,并決定2019年只生產該產品1萬臺,且預計2019年可獲利32(百萬元);但生產部門發現,若用預計的2019年的數據與2014-2018年中考核優秀年份的數據重新建立回歸方程,只有當重新估算的
①.現該公司計劃從2019年開始轉型,并決定2019年只生產該產品1萬臺,且預計2019年可獲利32(百萬元);但生產部門發現,若用預計的2019年的數據與2014-2018年中考核優秀年份的數據重新建立回歸方程,只有當重新估算的![]() ,
,![]() 的值(精確到0.01),相對于①中
的值(精確到0.01),相對于①中![]() ,
,![]() 的值的誤差的絕對值都不超過
的值的誤差的絕對值都不超過![]() 時,2019年該產品返修率才可低于千分之一.若生產部門希望2019年考核優秀,能否同意2019年只生產該產品1萬臺?請說明理由.
時,2019年該產品返修率才可低于千分之一.若生產部門希望2019年考核優秀,能否同意2019年只生產該產品1萬臺?請說明理由.
(參考公式:![]() ,
,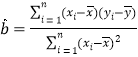
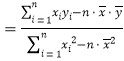 ,
,![]() ,
,![]() 相對
相對![]() 的誤差為
的誤差為![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 ,若點
,若點![]() 在橢圓C上,則點
在橢圓C上,則點![]() 稱為點M的一個“橢點”.
稱為點M的一個“橢點”.
(1)求橢圓C的標準方程;
(2)若直線![]() 與橢圓C相交于A,B兩點,且A,B兩點的“橢點”分別為P,Q,以PQ為直徑的圓經過坐標原點,試判斷
與橢圓C相交于A,B兩點,且A,B兩點的“橢點”分別為P,Q,以PQ為直徑的圓經過坐標原點,試判斷![]() 的面積是否為定值?若為定值,求出定值;若不為定值,說明理由.
的面積是否為定值?若為定值,求出定值;若不為定值,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點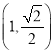 ,
,![]() 是該橢圓的左、右焦點,
是該橢圓的左、右焦點,![]() 是上頂點,且
是上頂點,且![]() 是等腰直角三角形.
是等腰直角三角形.
(1)求![]() 的方程;
的方程;
(2)已知![]() 是坐標原點,直線
是坐標原點,直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,點
兩點,點![]() 在
在![]() 上且滿足四邊形
上且滿足四邊形![]() 是一個平行四邊形,求
是一個平行四邊形,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是橢圓
是橢圓![]() 上的點,
上的點,![]() 是焦點,離心率
是焦點,離心率![]() .
.
(1)求橢圓的標準方程;
(2)設![]() 是橢圓上的兩點,且
是橢圓上的兩點,且![]() ,問線段
,問線段![]() 的垂直平分線是否過定點?若過定點,求出此定點的坐標,若不過定點,說明理由.
的垂直平分線是否過定點?若過定點,求出此定點的坐標,若不過定點,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某度假酒店為了解會員對酒店的滿意度,從中抽取50名會員進行調查,把會員對酒店的“住宿滿意度”與“餐飲滿意度”都分為五個評分標準:1分(很不滿意);2分(不滿意);3分(一般);4分(滿意);5分(很滿意).其統計結果如下表(住宿滿意度為![]() ,餐飲滿意度為
,餐飲滿意度為![]() )
)
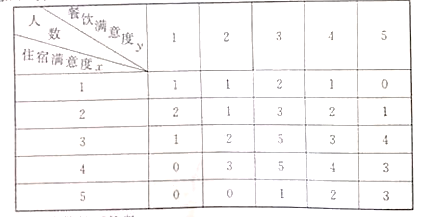
(1)求“住宿滿意度”分數的平均數;
(2)求“住宿滿意度”為3分時的5個“餐飲滿意度”人數的方差;
(3)為提高對酒店的滿意度,現從![]() 且
且![]() 的會員中隨機抽取2人征求意見,求至少有1人的“住宿滿意度”為2的概率.
的會員中隨機抽取2人征求意見,求至少有1人的“住宿滿意度”為2的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
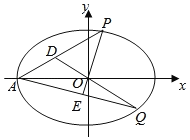
【題目】已知在平面直角坐標系xOy中,橢圓C:![]() (a>b>0)離心率為
(a>b>0)離心率為![]() ,其短軸長為2.
,其短軸長為2.
(1)求橢圓C的標準方程;
(2)如圖,A為橢圓C的左頂點,P,Q為橢圓C上兩動點,直線PO交AQ于E,直線QO交AP于D,直線OP與直線OQ的斜率分別為k1,k2,且k1k2=![]() ,
,![]()
![]() (λ,μ為非零實數),求λ2+μ2的值.
(λ,μ為非零實數),求λ2+μ2的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-5:不等式選講]
已知函數f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求實數a的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com