
【題目】四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形, ![]() .側面
.側面![]() 底面
底面![]() .
.
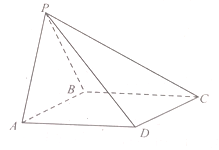
(1)證明: ![]() ;
;
(2)設![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析(2)![]()
【解析】【試題分析】(1)設![]() 中點為
中點為![]() ,連接
,連接![]() ,由已知
,由已知![]() ,所以
,所以![]() ,根據面面垂直的性質定理,有
,根據面面垂直的性質定理,有![]() 平面
平面![]() ,以
,以![]() 為原點,
為原點, ![]() 為
為![]() 軸,
軸, ![]() 為
為![]() 軸,建立空間直角坐標系,計算
軸,建立空間直角坐標系,計算![]() 可得證.(2)設
可得證.(2)設![]() ,利用直線
,利用直線![]() 和平面
和平面![]() 所成角為
所成角為![]() ,計算
,計算![]() ,再利用平面
,再利用平面![]() 和平面
和平面![]() 的法向量計算二面角的余弦值.
的法向量計算二面角的余弦值.
【試題解析】
解:(1)證法一:設![]() 中點為
中點為![]() ,連接
,連接![]() ,
,
由已知![]() ,所以
,所以![]() ,
,
而平面![]() 平面
平面![]() ,交線為
,交線為![]()
故![]() 平面
平面![]()
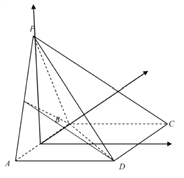
以![]() 為原點,
為原點, ![]() 為
為![]() 軸,
軸, ![]() 為
為![]() 軸,如圖建立空間直角坐標系,并設
軸,如圖建立空間直角坐標系,并設![]() ,
,
則![]()
所以![]()
![]() ,所以
,所以![]() .
.
證法二:設![]() 中點為
中點為![]() ,連接
,連接![]() ,由已知
,由已知![]() ,所以
,所以![]() ,
,
而平面![]() 平面
平面![]() ,交線為
,交線為![]()
故![]() 平面
平面![]() ,從而
,從而![]() ①
①
在矩形![]() 中,連接
中,連接![]() ,設
,設![]() 與
與![]() 交于
交于![]() ,
,
則由![]() 知
知![]() ,所以
,所以![]()
所以![]() ,故
,故![]() ②
②
由①②知![]() 平面
平面![]()
所以![]() .
.
(2)由![]() ,平面
,平面![]() 平面
平面![]() ,交線為
,交線為![]() ,可得
,可得![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,交線為
,交線為![]()
過![]() 作
作![]() ,垂足為
,垂足為![]() ,則
,則![]() 平面
平面![]()
![]() 與平面
與平面![]() 所成的角即為角
所成的角即為角![]()
所以![]()
從而三角形![]() 為等邊三角形,
為等邊三角形, ![]()
(也可以用向量法求出![]() ,設
,設![]() ,則
,則![]() ,可求得平面
,可求得平面![]() 的一個法向量為
的一個法向量為![]() ,而
,而![]() ,由
,由![]() 可解得
可解得![]() )
)
設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則![]() ,
,
![]() , 可取
, 可取![]()
設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則![]() ,
,
![]() ,可取
,可取![]()
于是![]() ,
,
故二面角![]() 的余弦值為
的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某地![]() 戶家庭的年收入
戶家庭的年收入![]() (萬元)和年飲食支出
(萬元)和年飲食支出![]() (萬元)的統計資料如下表:
(萬元)的統計資料如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 關于
關于![]() 的線性回歸方程;(結果保留到小數點后
的線性回歸方程;(結果保留到小數點后![]() 為數字)
為數字)
(2)利用(1)中的回歸方程,分析這![]() 戶家庭的年飲食支出的變化情況,并預測該地年收入
戶家庭的年飲食支出的變化情況,并預測該地年收入![]() 萬元的家庭的年飲食支出.(結果保留到小數點后
萬元的家庭的年飲食支出.(結果保留到小數點后![]() 位數字)
位數字)
附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
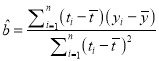 ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,圓
中,圓![]() 的圓心為
的圓心為![]() .已知點
.已知點![]() ,且
,且![]() 為圓
為圓![]() 上的動點,線段
上的動點,線段![]() 的中垂線交
的中垂線交![]() 于點
于點![]() .
.
(Ⅰ)求點![]() 的軌跡方程;
的軌跡方程;
(Ⅱ)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,拋物線
,拋物線![]() :
: ![]() 的焦點為
的焦點為![]() .
.![]() ,
, ![]() 是過點
是過點![]() 互相垂直的兩條直線,直線
互相垂直的兩條直線,直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,直線
兩點,直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐![]() ,
, ![]() 平面
平面![]() ,底面
,底面![]() 中,
中, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 為
為![]() 的中點.
的中點.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)問在棱![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 平面
平面![]() ,若存在,請求出二面角
,若存在,請求出二面角![]() 的余弦值;若不存在,請說明理由.
的余弦值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】微信是當前主要的社交應用之一,有著幾億用戶,覆蓋范圍廣,及時快捷,作為移動支付的重要形式,微信支付成為人們支付的重要方式和手段。某公司為了解人們對“微信支付”認可度,對![]() 年齡段的人群隨機抽取
年齡段的人群隨機抽取![]() 人進行了一次“你是否喜歡微信支付”的問卷調查,根據調查結果得到如下統計表和各年齡段人數頻率分布直方圖:
人進行了一次“你是否喜歡微信支付”的問卷調查,根據調查結果得到如下統計表和各年齡段人數頻率分布直方圖:
組號 | 分組 | 喜歡微信支付的人數 | 喜歡微信支付的人數 占本組的頻率 |
第一組 |
|
|
|
第二組 |
|
|
|
第三組 |
|
|
|
第四組 |
|
|
|
第五組 |
|
|
|
第六組 |
|
|
|

(1)補全頻率分布直方圖,并求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)在第四、五、六組“喜歡微信支付”的人中,用分層抽樣的方法抽取![]() 人參加“微信支付日鼓勵金”活動,求第四、五、六組應分別抽取的人數;
人參加“微信支付日鼓勵金”活動,求第四、五、六組應分別抽取的人數;
(3)在(2)中抽取的![]() 人中隨機選派
人中隨機選派![]() 人做采訪嘉賓,求所選派的
人做采訪嘉賓,求所選派的![]() 人沒有第四組人的概率.
人沒有第四組人的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com