
【題目】已知函數![]() .
.
(1)若m=0,求函數f(x)的定義域;
(2)若函數f(x)的值域為R,求實數m的取值范圍;
(3)若函數f(x)在區間![]() 上是增函數,求實數m的取值范圍.
上是增函數,求實數m的取值范圍.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】設f(x)與g(x)是定義在同一區間[a,b]上的兩個函數,若函數y=f(x)-g(x)在x∈[a,b]上有兩個不同的零點,則稱f(x)和g(x)在[a,b]上是“關聯函數”,區間[a,b]稱為“關聯區間”.若f(x)=x2-3x+4與g(x)=2x+m在[0,3]上是“關聯函數”,則m的取值范圍是 ( ).
A. ![]() B.[-1,0] C.(-∞,-2] D.
B.[-1,0] C.(-∞,-2] D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四邊形ABCD滿足AB⊥AD,BC∥AD且BC=4,點M為PC的中點,點E為BC邊上的點,且 ![]() =λ.
=λ. 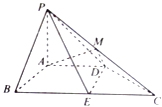
(1)求證:平面ADM⊥平面PBC;
(2)是否存在實數λ,使得二面角P﹣DE﹣B的余弦值為 ![]() ?若存在,求出實數λ的值,若不存在,請說明理由.
?若存在,求出實數λ的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=![]() 滿足:對任意的實數x1≠x2,都有(x1-x2)[f(x1)-f(x2)]>0成立,則實數a的取值范圍是( )
滿足:對任意的實數x1≠x2,都有(x1-x2)[f(x1)-f(x2)]>0成立,則實數a的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設全集U=R,集合A={x|2x-1≥1},B={x|x2-4x-5<0}.
(Ⅰ)求A∩B,(UA)∪(UB);
(Ⅱ)設集合C={x|m+1<x<2m-1},若B∩C=C,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正方形![]() 的棱長為1,點
的棱長為1,點![]() 分別是棱
分別是棱![]() 的中點.
的中點.
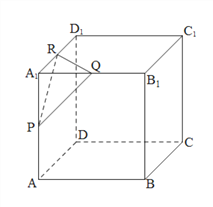
(Ⅰ)求二面角![]() 的余弦值;
的余弦值;
(Ⅱ)以![]() 為底面作正三棱柱,若此三棱柱另一底面三個頂點也都在該正方體的表面上,求這個正三棱柱的高.
為底面作正三棱柱,若此三棱柱另一底面三個頂點也都在該正方體的表面上,求這個正三棱柱的高.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某食品企業一個月內被消費者投訴的次數用![]() 表示.據統計,隨機變量
表示.據統計,隨機變量![]() 的概率分布如下表所示.
的概率分布如下表所示.
| 0 | 1 | 2 | 3 |
| 0.1 | 0.3 |
|
|
(1)求![]() 的值和
的值和![]() 的數學期望;
的數學期望;
(2)假設一月份與二月份被消費者投訴的次數互不影響,求該企業在這兩個月內共被消費者投訴2次的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com