
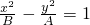 在同一坐標系下的圖象可能是
在同一坐標系下的圖象可能是
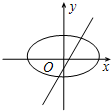

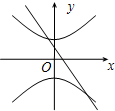
分析:通過討論A,B的值,得到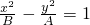 表示的圓錐曲線形狀;將直線方程Bx-y+A=0變形為斜截式判斷出其斜率及縱截距,由兩種曲線的特點,選出圖象.
表示的圓錐曲線形狀;將直線方程Bx-y+A=0變形為斜截式判斷出其斜率及縱截距,由兩種曲線的特點,選出圖象.
解答:當A>0,B>0時,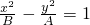 表示焦點在x軸的雙曲線
表示焦點在x軸的雙曲線
方程Bx-y+A=0即為y=Bx+A其斜率為B,縱截距為A
∴選項C,D錯
當A<0,B>0,且|A|>|B|時,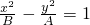 表示焦點在y軸的橢圓
表示焦點在y軸的橢圓
方程Bx-y+A=0即為y=Bx+A其斜率為B,縱截距為A
故選項A錯
當A<0,B>0,且|A|<|B|時,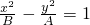 表示焦點在x軸的橢圓
表示焦點在x軸的橢圓
方程Bx-y+A=0即為y=Bx+A其斜率為B,縱截距為A
故選B
點評:解決已知曲線的方程選擇其圖象的題目,一般先根據(jù)方程研究方程表示的曲線的性質(zhì),再根據(jù)曲線的性質(zhì)選擇出合適的圖象.


科目:高中數(shù)學 來源: 題型:
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
| a |
| x |
| b |
| y |
| 2 |
| x |
| 9 |
| 1-2x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數(shù)學 來源:2014屆山東省淄博市高二下學期期中模塊檢測文科數(shù)學試卷(解析版) 題型:選擇題
用反證法證明命題“設a,b∈R,|a|+|b|<1,a2-4b≥0,那么x2+ax+b=0的兩根的絕對值都小于1”時,應假設
A.方程x2+ax+b=0的兩根的絕對值存在一個小于1
B.方程x2+ax+b=0的兩根的絕對值至少有一個大于等于1
C.方程x2+ax+b=0沒有實數(shù)根
D.方程x2+ax+b=0的兩根的絕對值都不小于1
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com