
| A. | $\frac{7}{8}$ | B. | -$\frac{7}{8}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
分析 根據二倍角公式和根據同角三角函數關系式即可求解.
解答 解:由$\frac{cos2α}{cos(α+\frac{π}{4})}$=$\frac{1}{2}$,
可得:2cos2α=cos($α+\frac{π}{4}$)
得:4cos22α=cos2($α+\frac{π}{4}$)
∵cos2($α+\frac{π}{4}$)=2cos2($α+\frac{π}{4}$)-1,即1-sin2α=2cos2($α+\frac{π}{4}$)
∴8cos22α=1-sin2α
由cos22α+sin22α=1.
∴8(1-sin22α)=1-sin2α
解得:sin2α=$-\frac{7}{8}$.
故選:B.
點評 本題主要考察了同角三角函數關系式和二倍角公式的靈活應用,屬于基本知識的考查.


科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 2$\sqrt{13}$ | C. | 2$\sqrt{5}$ | D. | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 1+3 | C. | 1+3+5 | D. | 1+3+5+7 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p是假命題 | B. | q是真命題 | C. | p(∧¬q) 是真命題 | D. | (¬p)∧q是真命題 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
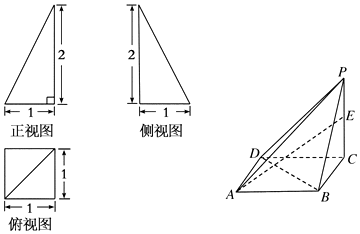
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 10 | B. | -10 | C. | -14 | D. | 無法確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
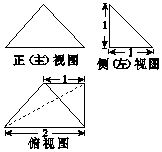
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com