
| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ |
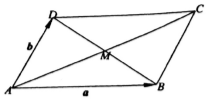
分析 根據向量加法、減法的運算法則,可得$\overrightarrow{BD}$=$\overrightarrow{AD}$-$\overrightarrow{AB}$,再根據平行四邊形的對角線互相平分,可得$\overrightarrow{MD}$=$\frac{1}{2}$$\overrightarrow{BD}$,即可得到本題的答案.
解答 解:∵平行四邊形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,
∴$\overrightarrow{BD}$=$\overrightarrow{AD}$-$\overrightarrow{AB}$=$\overrightarrow{b}$-$\overrightarrow{a}$,
∵兩條對角線相交于點M,可得M是AC、BD的中點
∴$\overrightarrow{MD}$=$\frac{1}{2}$$\overrightarrow{BD}$=$\frac{1}{2}$($\overrightarrow{b}$-$\overrightarrow{a}$)=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$,
故選:D
點評 本題考查的知識點是平面向量在幾何中的應用,向量的線性運算,平行四邊形的性質,難度中檔.


 英才點津系列答案
英才點津系列答案 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | $\frac{8}{9}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
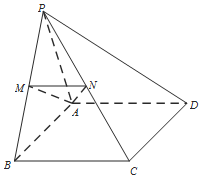 在四棱錐P-ABCD中,△PAB為正三角形,四邊形ABCD為矩形,平面PAB⊥平面ABCD,AB=2AD,M,N分別為PB,PC中點.
在四棱錐P-ABCD中,△PAB為正三角形,四邊形ABCD為矩形,平面PAB⊥平面ABCD,AB=2AD,M,N分別為PB,PC中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com