
| A. | f(49)<f(64)<f(81) | B. | f(49)<f(81)<f(64) | C. | f(64)<f(49)<f(81) | D. | f(64)<f(81)<f(49) |
分析 根據題意,由f(x-3)=-f(x)分析可得f(x-6)=-f(x-3)=f(x),則函數f(x)是周期為6的函數,進而可得f(49)=f(1+6×8)=f(1),f(81)=f(-3+6×14)=f(-3),f(64)=f(-2+6×11)=f(-2),進而結合函數的奇偶性可得則f(49)=f(1+6×8)=f(1),f(81)=f(-3)=f(3),f(64)=f(-2)=f(2),進而結合題意分析可得函數f(x)在區間[0,3]上為增函數,進而有f(1)<f(2)<f(3),即f(49)<f(64)<f(81);即可得答案.
解答 解:根據題意,函數f(x)滿足f(x-3)=-f(x),
有f(x-6)=-f(x-3)=f(x),則函數f(x)是周期為6的函數,
f(49)=f(1+6×8)=f(1),
f(81)=f(-3+6×14)=f(-3),
f(64)=f(-2+6×11)=f(-2),
又由函數為偶函數,則f(49)=f(1+6×8)=f(1),
f(81)=f(-3)=f(3),
f(64)=f(-2)=f(2),
又由對?x1,x2∈[0,3]且x1≠x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,
則函數f(x)在區間[0,3]上為增函數,
進而有f(1)<f(2)<f(3),
即f(49)<f(64)<f(81);
故選:A
點評 本題考查函數奇偶性與單調性的綜合運用,涉及函數周期性的判定與應用,注意由$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0判斷出函數的單調性.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | $±\sqrt{2}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | 以上答案都不對 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2015 | B. | $\frac{2015}{2}$ | C. | 2014 | D. | 1007 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | m | C. | 2m | D. | 4m |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
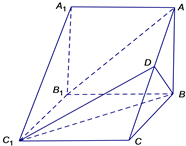 如圖,在三棱柱ABC-A1B1C1中,側棱AA1⊥底面ABC,AA1=AB=2,AB⊥BC,BC=3.
如圖,在三棱柱ABC-A1B1C1中,側棱AA1⊥底面ABC,AA1=AB=2,AB⊥BC,BC=3.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,在平面直角坐標系中有三條直線l1,l2,l3,其對應的斜率分別為k1,k2,k3,則下列選項中正確的是( )
如圖,在平面直角坐標系中有三條直線l1,l2,l3,其對應的斜率分別為k1,k2,k3,則下列選項中正確的是( )| A. | k3>k1>k2 | B. | k1-k2>0 | C. | k1•k2<0 | D. | k3>k2>k1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com