
分析 (1)利用冪函數經過的點,求解函數的解析式,利用奇偶性的定義判斷即可.
(2)利用函數單調性的定義證明即可;
(3)畫出函數的圖象即可.
解答 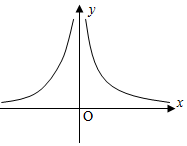 解:(1)依題得:$\frac{1}{3}$=$(\sqrt{3})^{m}$,m=-2.
解:(1)依題得:$\frac{1}{3}$=$(\sqrt{3})^{m}$,m=-2.
故f(x)=x-2.…(3分)
f(-x)=(-x)-2=$\frac{1}{{x}^{2}}$=x-2=f(x),
所以,f(x)是偶函數…(4分)
(2)假設任意x1<x2<0
f(x1)-f(x2)=x1-2-x2-2=$\frac{{{x}_{2}}^{2}-{{x}_{1}}^{2}}{{{x}_{1}}^{2}{{x}_{2}}^{2}}$=$\frac{({x}_{1}+{x}_{2})({x}_{2}{-x}_{1})}{{{x}_{1}}^{2}{{x}_{2}}^{2}}$<0,
∴f(x1)<f(x2)
∴f(x)在(-∞,0)上是增函數.…(8分)
(3)如圖.…(12分)
點評 本題考查函數的圖象的畫法,函數的單調性以及函數的奇偶性的判斷與應用,考查計算能力.


 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|-3<x<0或x>3} | B. | { x|x<-3或0<x<3} | C. | { x|x<-3或x>3} | D. | { x|-3<x<0或0<x<3} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
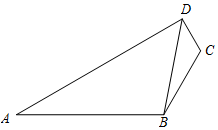 如圖,已知A,B,C,D四點共面,且CD=1,BC=2,AB=4,∠ABC=120°,cos∠BDC=$\frac{{2\sqrt{7}}}{7}$.
如圖,已知A,B,C,D四點共面,且CD=1,BC=2,AB=4,∠ABC=120°,cos∠BDC=$\frac{{2\sqrt{7}}}{7}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com