
【題目】棉花的優質率是以其纖維長度來街量的,纖維越長的棉花晶質越高.棉花的品質分類標準為:纖維長度小于等于![]() 的為粗絨棉,纖維長度在
的為粗絨棉,纖維長度在![]() 的為細絨棉,纖維長度大于
的為細絨棉,纖維長度大于![]() 的為長絨棉,其中纖維長度在
的為長絨棉,其中纖維長度在![]() 以上的棉花又名“軍海1號”.某采購商從新疆某一棉花基地抽測了
以上的棉花又名“軍海1號”.某采購商從新疆某一棉花基地抽測了![]() 根棉花的纖維長度,得到數據如下圖頻率分布表所示:
根棉花的纖維長度,得到數據如下圖頻率分布表所示:
纖維長度 |
|
|
|
|
根數 |
|
|
|
|
(1)若將頻率作為概率, 根據以上數據,能否認為該基地的這批棉花符合“長絨棉占全部棉花的![]() 以上”的要求?
以上”的要求?
(2)用樣本估計總體, 若這批榨花共有![]() ,基地提出了兩種銷售方案給采購商參考.方案一:不分等級賣出,每千克按
,基地提出了兩種銷售方案給采購商參考.方案一:不分等級賣出,每千克按![]() 元計算,方案二:對
元計算,方案二:對![]() 棉花先分等級再銷售,分級后不同等級的棉花售價如下表:
棉花先分等級再銷售,分級后不同等級的棉花售價如下表:
纖維長度 |
|
|
|
|
售價 |
|
|
|
|
從來購商的角度,請你幫他決策一下該用哪個方案.
(3)用分層抽樣的方法從長絨棉中抽取6根棉花,再從此![]() 根棉花中抽取兩根進行檢驗.求抽到的兩根棉花只有一根是“軍海1號”的概率.
根棉花中抽取兩根進行檢驗.求抽到的兩根棉花只有一根是“軍海1號”的概率.
【答案】(1)可以認為該基地的這批棉花符合“長絨棉占全部棉花的![]() 以上;
以上;
(2)選方案一更好;(3)![]() .
.
【解析】
(1)由題意可得長絨棉的頻數
(2)分別求出方案一與方案二所花的錢數,對比可得答案;
(3)求出從![]() 根棉花中抽取兩根進行檢驗,可得總的抽取方法數與抽到的兩根棉花只有一根起“軍海1號”的抽取方法數,可得抽到的兩根棉花只有一根是“軍海1號”的概率.
根棉花中抽取兩根進行檢驗,可得總的抽取方法數與抽到的兩根棉花只有一根起“軍海1號”的抽取方法數,可得抽到的兩根棉花只有一根是“軍海1號”的概率.
解:由題意可得長絨棉的頻數為:![]() ,
,
故![]() ,故可以認為該基地的這批棉花符合“長絨棉占全部棉花的
,故可以認為該基地的這批棉花符合“長絨棉占全部棉花的![]() 以上;
以上;
(2)由題意可得方案一需花費:![]() 元;
元;
方案二需花費:![]() .
.
所以,選方案一更好;
(3) 由題意結合用分層抽樣的方法從長絨棉中抽取6根棉花,可得抽取的長絨棉為:![]() 根,抽取的軍海1號為:
根,抽取的軍海1號為:![]() 根,
根,
再從此![]() 根棉花中抽取兩根進行檢驗,可得總的抽取方法有
根棉花中抽取兩根進行檢驗,可得總的抽取方法有![]() 種,
種,
其中抽到的兩根棉花只有一根是“軍海1號”的抽取方法有![]() 種,
種,
故抽到的兩根棉花只有一根是“軍海1號”的概率為:![]() .
.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的傾斜角為
的傾斜角為![]() ,且經過點
,且經過點![]() .以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,直線
.以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,直線![]() ,從原點O作射線交
,從原點O作射線交![]() 于點M,點N為射線OM上的點,滿足
于點M,點N為射線OM上的點,滿足![]() ,記點N的軌跡為曲線C.
,記點N的軌跡為曲線C.
(Ⅰ)求出直線![]() 的參數方程和曲線C的直角坐標方程;
的參數方程和曲線C的直角坐標方程;
(Ⅱ)設直線![]() 與曲線C交于P,Q兩點,求
與曲線C交于P,Q兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解本學期學生參加公益勞動的情況,某校從初高中學生中抽取100名學生,收集了他們參加公益勞動時間(單位:小時)的數據,繪制圖表的一部分如表.
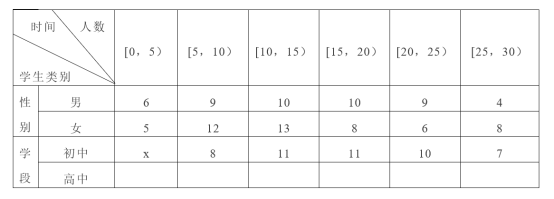
(1)從男生中隨機抽取一人,抽到的男生參加公益勞動時間在![]() 的概率:
的概率:
(2)從參加公益勞動時間![]() 的學生中抽取3人進行面談,記
的學生中抽取3人進行面談,記![]() 為抽到高中的人數,求
為抽到高中的人數,求![]() 的分布列;
的分布列;
(3)當![]() 時,高中生和初中生相比,那學段學生平均參加公益勞動時間較長.(直接寫出結果)
時,高中生和初中生相比,那學段學生平均參加公益勞動時間較長.(直接寫出結果)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的點,
上的點,![]() 的面積最大值為
的面積最大值為![]() ,直線
,直線![]() 與
與![]() 交于
交于![]() 兩點,且
兩點,且![]() (
(![]() 為坐標原點)
為坐標原點)
(1)求橢圓![]() 的方程;
的方程;
(2)求證:![]() 到直線
到直線![]() 的距離為定值,并求其定值.
的距離為定值,并求其定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,四邊形
中,四邊形![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中點.
的中點.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值為
的余弦值為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】超級病菌是一種耐藥性細菌,產生超級細菌的主要原因是用于抵抗細菌侵蝕的藥物越來越多,但是由于濫用抗生素的現象不斷的發生,很多致病菌也對相應的抗生素產生了耐藥性,更可怕的是,抗生素藥物對它起不到什么作用,病人會因為感染而引起可怕的炎癥,高燒、痙攣、昏迷直到最后死亡.某藥物研究所為篩查某種超級細菌,需要檢驗血液是否為陽性,現有n(![]() )份血液樣本,每個樣本取到的可能性均等,有以下兩種檢驗方式:
)份血液樣本,每個樣本取到的可能性均等,有以下兩種檢驗方式:
(1)逐份檢驗,則需要檢驗n次;
(2)混合檢驗,將其中k(![]() 且
且![]() )份血液樣本分別取樣混合在一起檢驗,若檢驗結果為陰性,這k份的血液全為陰性,因而這k份血液樣本只要檢驗一次就夠了,如果檢驗結果為陽性,為了明確這k份血液究竟哪幾份為陽性,就要對這k份再逐份檢驗,此時這k份血液的檢驗次數總共為
)份血液樣本分別取樣混合在一起檢驗,若檢驗結果為陰性,這k份的血液全為陰性,因而這k份血液樣本只要檢驗一次就夠了,如果檢驗結果為陽性,為了明確這k份血液究竟哪幾份為陽性,就要對這k份再逐份檢驗,此時這k份血液的檢驗次數總共為![]() 次,假設在接受檢驗的血液樣本中,每份樣本的檢驗結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為p(
次,假設在接受檢驗的血液樣本中,每份樣本的檢驗結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為p(![]() ).
).
(1)假設有5份血液樣本,其中只有2份樣本為陽性,若采用逐份檢驗方式,求恰好經過2次檢驗就能把陽性樣本全部檢驗出來的概率;
(2)現取其中k(![]() 且
且![]() )份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數為
)份血液樣本,記采用逐份檢驗方式,樣本需要檢驗的總次數為![]() ,采用混合檢驗方式,樣本需要檢驗的總次數為
,采用混合檢驗方式,樣本需要檢驗的總次數為![]() .
.
(i)試運用概率統計的知識,若![]() ,試求p關于k的函數關系式
,試求p關于k的函數關系式![]() ;
;
(ii)若![]() ,采用混合檢驗方式可以使得樣本需要檢驗的總次數的期望值比逐份檢驗的總次數期望值更少,求k的最大值.
,采用混合檢驗方式可以使得樣本需要檢驗的總次數的期望值比逐份檢驗的總次數期望值更少,求k的最大值.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 與
與![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 的交于
的交于![]() 點,
點,![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,求
兩點,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com