
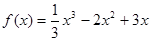 (
(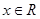 )的圖象為曲線
)的圖象為曲線 .
. 上任意一點處的切線的斜率的取值范圍;
上任意一點處的切線的斜率的取值范圍;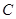 上存在兩點處的切線互相垂直,求其中一條切線與曲線
上存在兩點處的切線互相垂直,求其中一條切線與曲線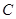 的切點的橫坐標的取值范圍;
的切點的橫坐標的取值范圍;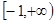 (2)
(2) 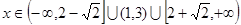 (3) 不存在一條直線與曲線C同時切于兩點
(3) 不存在一條直線與曲線C同時切于兩點 ,則
,則 ,
,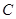 上任意一點處的切線的斜率的取值范圍是
上任意一點處的切線的斜率的取值范圍是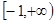 ;------------3分
;------------3分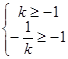 ---------------------------------------------------------5分
---------------------------------------------------------5分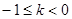 或
或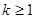 ,由
,由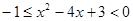 或
或
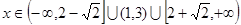 ;-------------------------------7分
;-------------------------------7分 的切線曲線C同時切于兩點,另一切點為B
的切線曲線C同時切于兩點,另一切點為B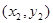 ,
, ,
,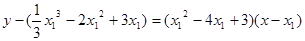 ,
,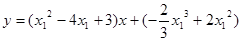 ,
,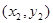 的切線方程是
的切線方程是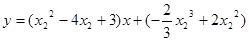 ,
,  ,得
,得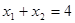 ,----------------------11分
,----------------------11分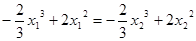 ,
,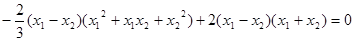
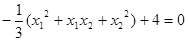 ,即
,即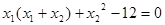
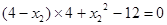 ,
,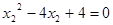
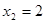 ,但當
,但當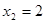 時,由
時,由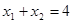 得
得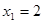 ,這與
,這與 矛盾。
矛盾。

 備戰中考寒假系列答案
備戰中考寒假系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com