
分析 依題意,設雙曲線的方程為9x2-16y2=λ,將點$(2\sqrt{3},-3)$,代入可求λ,即可求出雙曲線的方程.
解答 解:設與雙曲線$\frac{x^2}{16}-\frac{y^2}{9}=1$有共同的漸近線的雙曲線的方程為9x2-16y2=λ,
∵該雙曲線經過點$(2\sqrt{3},-3)$,
∴λ=9×12-16×9=-36.
∴所求的雙曲線方程為:9x2-16y2=-36,即$\frac{y^2}{{\frac{9}{4}}}-\frac{x^2}{4}=1$
故答案為:$\frac{y^2}{{\frac{9}{4}}}-\frac{x^2}{4}=1$.
點評 本題考查雙曲線的簡單性質,設出所求雙曲線的方程為9x2-16y2=λ是關鍵,屬于中檔題.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
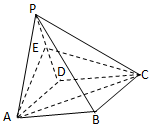 在四棱錐P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中點.
在四棱錐P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com