
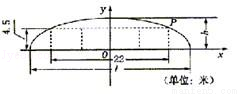
(2003•上海)如圖,某隧道設計為雙向四車道,車道總寬22米,要求通行車輛限高4.5米,隧道全長2.5千米,隧道的拱線近似地看成半個橢圓形狀.
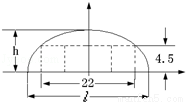
(1)若最大拱高h為6米,則隧道設計的拱寬l是多少?
(2)若最大拱高h不小于6米,則應如何設計拱高h和拱寬l,才能使半個橢圓形隧道的土方工程量最最小?(半個橢圓的面積公式為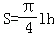 ,柱體體積為:底面積乘以高.本題結果精確到0.1米)
,柱體體積為:底面積乘以高.本題結果精確到0.1米)
(1)33.3米;(2)故當拱高約為6.4米、拱寬約為31.1米時,土方工程量最小.
【解析】
試題分析:(1)根據題意,建立坐標系,可得P的坐標并設出橢圓的方程,將b=h=6與點P坐標代入橢圓方程,得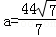 ,依題意,可得l=2a,計算可得答案;
,依題意,可得l=2a,計算可得答案;
(2)根據題意,設橢圓方程為 ,將(11,4.5)代入方程可得
,將(11,4.5)代入方程可得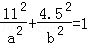 ,結合基本不等式可得
,結合基本不等式可得 ,分析可得當ab≥99且l=2a,h=b時,
,分析可得當ab≥99且l=2a,h=b時, ,進而分析可得答案.
,進而分析可得答案.
【解析】
(1)如圖建立直角坐標系,則點P(11,4.5),
橢圓方程為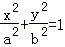 .
.
將b=h=6與點P坐標代入橢圓方程,
得 ,
,
此時此時
因此隧道的拱寬約為33.3米;
(2)由橢圓方程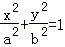 ,
,
根據題意,將(11,4.5)代入方程可得 .
.
因為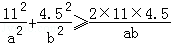
即ab≥99且l=2a,h=b,
所以
當S取最小值時,
有 ,
,
得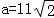 ,
,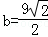
此時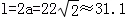 ,h=b≈6.4
,h=b≈6.4
故當拱高約為6.4米、拱寬約為31.1米時,土方工程量最小.


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源:[同步]2014年蘇教版必修一 1.2 子集、全集、補集練習卷(解析版) 題型:選擇題
設集合A={1,4,x},B={1,x2},且B⊆A,則滿足條件的實數x的個數有( )
A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
科目:高中數學 來源:[同步]2014年湘教版選修1-1 3.2導數的運算練習卷(解析版) 題型:填空題
設函數 ,集合M={x|f(x)<0},P={x|f′(x)>0},若M⊆P,則實數a的取值范圍是 .
,集合M={x|f(x)<0},P={x|f′(x)>0},若M⊆P,則實數a的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源:[同步]2014年湘教版選修1-1 3.1 導數的概念練習卷(解析版) 題型:填空題
在曲線y=x2+1的圖象上取一點(1,2)及附近一點(1+△x,2+△y),則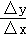 為 .
為 .
查看答案和解析>>
科目:高中數學 來源:[同步]2014年湘教版選修1-1 2.4 圓錐曲線的應用練習卷(解析版) 題型:解答題
根據我國汽車制造的現實情況,一般卡車高3 m,寬1.6 m.現要設計橫斷面為拋物線型的雙向二車道的公路隧道,為保障雙向行駛安全,交通管理規定汽車進入隧道后必須保持距中線0.4 m的距離行駛.已知拱口AB寬恰好是拱高OC的4倍,若拱寬為a m,求能使卡車安全通過的a的最小整數值.
查看答案和解析>>
科目:高中數學 來源:[同步]2014年湘教版選修1-1 2.4 圓錐曲線的應用練習卷(解析版) 題型:選擇題
(4分)如圖,花壇水池中央有一噴泉,水管OP=1m,水從噴頭P噴出后呈拋物線狀先向上至最高點后落下,若最高點距水面2m,P距拋物線對稱軸1m,則在水池直徑的下列可選值中,最合算的是( )

A.2.5m B.4m C.5m D.6m
查看答案和解析>>
科目:高中數學 來源:[同步]2014年湘教版選修1-1 2.1 橢圓練習卷(解析版) 題型:解答題
(2005•上海)點A、B分別是橢圓 +
+ =1長軸的左、右焦點,點F是橢圓的右焦點.點P在橢圓上,且位于x軸上方,PA⊥PF.
=1長軸的左、右焦點,點F是橢圓的右焦點.點P在橢圓上,且位于x軸上方,PA⊥PF.
(1)求P點的坐標;
(2)設M是橢圓長軸AB上的一點,M到直線AP的距離等于|MB|,求橢圓上的點到點M的距離d的最小值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com