
分析 根據不等式的基本性質,判斷題目中命題的真假性即可.
解答 解:對于①,若ab>0,則$\frac{1}{ab}$>0
又a>b,
∴$\frac{1}{b}$>$\frac{1}{b}$,∴$\frac{1}{a}$<$\frac{1}{b}$,∴①正確;
對于②,若a>|b|≥0,則a2>b2,∴②正確;
對于③,若a>b,c>d,則-c<-d,
∴-d>-c,∴a-d>b-c,
∴a-c>b-d不成立,③錯誤;
對于④,對于正數a,b,m,
若a<b,則$\frac{a}{b}<\frac{a+m}{b+m}$成立,
即a(b+m)<b(a+m)
∴am<bm,
∴a<b,④正確;
綜上,正確的命題序號是①②④.
故答案為:①②④.
點評 本題考查了不等式的基本性質與應用問題,也考查了命題真假的判斷問題,是中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 成功(人) | 失敗(人) | 合計 | |
| 20~30(歲) | 20 | 40 | 60 |
| 30~40(歲) | 50 | ||
| 合計 | 70 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 364 | B. | 365 | C. | 728 | D. | 730 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
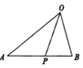 如圖,在△OAB,點P在邊AB上,且AP:PB=5:3,則$\overrightarrow{OP}$=( )
如圖,在△OAB,點P在邊AB上,且AP:PB=5:3,則$\overrightarrow{OP}$=( )| A. | $\frac{5}{8}$$\overrightarrow{OB}$+$\frac{3}{8}$$\overrightarrow{OA}$ | B. | $\frac{5}{8}$$\overrightarrow{OA}$+$\frac{3}{8}$$\overrightarrow{OB}$ | C. | $\frac{5}{8}$$\overrightarrow{OB}$-$\frac{3}{8}$$\overrightarrow{OA}$ | D. | $\frac{5}{8}$$\overrightarrow{OA}$-$\frac{3}{8}$$\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com