
設 圓
圓 與
與 軸正半軸的交點為
軸正半軸的交點為 ,與曲線
,與曲線 的交點為
的交點為 ,直線
,直線 與
與 軸的交點為
軸的交點為 .
.
(1)用 表示
表示 和
和
(2)若數列 滿足
滿足
(1)求常數 的值,使得數列
的值,使得數列 成等比數列;
成等比數列;
(2)比較 與
與 的大小.
的大小.
(1) ,
, ;(2)當
;(2)當 時,數列
時,數列 成公比為4的等比數列;當
成公比為4的等比數列;當 時,數列
時,數列 成公比為2的等比數列.
成公比為2的等比數列. .
.
【解析】
試題分析:本題主要考查曲線與圓相交問題、直線的方程、等比數列的證明、利用導數判斷函數的單調性等基礎知識,考查學生的分析問題解決問題的能力、轉化能力、計算能力.第一問,點N代入到曲線 和圓中,聯立得到
和圓中,聯立得到 ,由于直線MN過M、A點,從而得到直線MN的方程,N點也在MN上,代入MN方程中,經整理得到
,由于直線MN過M、A點,從而得到直線MN的方程,N點也在MN上,代入MN方程中,經整理得到 的表達式;第二問,(ⅰ)利用等比數列的定義知
的表達式;第二問,(ⅰ)利用等比數列的定義知 為等比數列,利用等比數列的通項公式,經過化簡得
為等比數列,利用等比數列的通項公式,經過化簡得 ,利用
,利用 的通項公式和
的通項公式和 為等比數列列出2個關系式,利用2個式子是q倍的關系,解出p和q的值;(ⅱ)利用
為等比數列列出2個關系式,利用2個式子是q倍的關系,解出p和q的值;(ⅱ)利用 可以猜想
可以猜想 ,即需要證
,即需要證 ,構造函數
,構造函數 ,利用導數判斷函數
,利用導數判斷函數 的單調性,從而確定
的單調性,從而確定 ,即
,即 ,所以
,所以 .
.
試題解析:(1) 與圓
與圓 交于點
交于點 ,則
,則 ,即
,即 .由題可知,點
.由題可知,點 的坐標為
的坐標為 ,從而直線
,從而直線 的方程為
的方程為 ,由點
,由點 在直線
在直線 上得
上得 ,將
,將 ,
, 代入,
代入,
得 ,
,
 即
即 4分
4分
(2)由 知,
知, 為等比數列,由
為等比數列,由 ,
, 知,公比為4,故
知,公比為4,故 ,所以
,所以 5分
5分
(1)


令 得
得

由等式
對于任意 成立,得
成立,得
 解得
解得 或
或 8分
8分
故當 時,數列
時,數列 成公比為4的等比數列;
成公比為4的等比數列;
當 時,數列
時,數列 成公比為2的等比數列. 9分
成公比為2的等比數列. 9分
(2)由(1)知 ,當
,當 時,
時,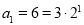 ;當
;當 時,
時, 事實上,令
事實上,令 ,則
,則 故
故
 是增函數,所以
是增函數,所以 ,即
,即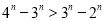
即 . 14分
. 14分
考點:曲線與圓相交問題、直線的方程、等比數列的證明、利用導數判斷函數的單調性.


科目:高中數學 來源:2013-2014學年福建省高三高考壓軸理科數學試卷(解析版) 題型:選擇題
下列命題正確的是( )
A.存在x0∈R,使得 的否定是:不存在x0∈R,使得
的否定是:不存在x0∈R,使得 ;
;
B.存在x0∈R,使得 的否定是:任意x∈R,均有
的否定是:任意x∈R,均有
C.若x=3,則x2-2x-3=0的否命題是:若x≠3,則x2-2x-3≠0.
D.若 為假命題,則命題p與q必一真一假
為假命題,則命題p與q必一真一假
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省福州市高三5月綜合練習文科數學試卷(解析版) 題型:選擇題
已知直線a,b異面, ,給出以下命題:①一定存在平行于a的平面
使 ;②一定存在平行于a的平面
;②一定存在平行于a的平面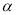 使
使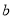 ∥
∥ ;③一定存在平行于a的平面
;③一定存在平行于a的平面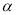 使
使 ;④一定存在無數個平行于a的平面
;④一定存在無數個平行于a的平面 與b交于一定點.則其中論斷正確的是( )
與b交于一定點.則其中論斷正確的是( )
A.①④ B.②③ C.①②③ D.②③④
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省高考考前模擬理科數學試卷(解析版) 題型:填空題
已知集合 ,若對于任意實數對
,若對于任意實數對 ,存在
,存在 ,使得
,使得 成立,則稱集合
成立,則稱集合 為“正交點集”,給出下列集合:
為“正交點集”,給出下列集合:
① ;②
;② ;③
;③ ;
;
④ ;⑤
;⑤ .
.
則滿足條件的“正交集合”有:_________________________(寫出所有滿足條件的集合的序號)
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省高考考前模擬理科數學試卷(解析版) 題型:選擇題
已知曲線 :
: 和
和 :
: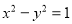 ,且曲線
,且曲線 的焦點分別為
的焦點分別為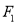 、
、 ,點
,點 是
是 和
和 的一個交點,則△
的一個交點,則△ 的形狀是( )
的形狀是( )
A.銳角三角形 B.直角三角形 C.鈍角三角形 D.都有可能
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省廈門市高三5月適應性考試理科數學試卷(解析版) 題型:選擇題
已知圓 和圓
和圓 ,動圓M與圓
,動圓M與圓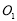 ,圓
,圓 都相切,動圓的圓心M的軌跡為兩個橢圓,這兩個橢圓的離心率分別為
都相切,動圓的圓心M的軌跡為兩個橢圓,這兩個橢圓的離心率分別為 ,
, (
(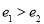 ),則
),則 的最小值是( )
的最小值是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com