【題目】記矩陣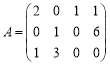
中的第
行第
列上的元素為
，現對矩陣
中的元素按如下算法所示的步驟作變動（直到不能變動為止）：若
，則
，
，
，若
，則不變動，這樣得到矩陣B，再對矩陣B中的元素按如下算法所示的步驟作變動（直到不能變動為止）：若
，則
，
，
；若
，則不變動，這樣得到矩陣
，則
________；
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】中國古代數學經典《九章算術》系統地總結了戰國、秦、漢時期的數學成就，書中將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬，將四個面都為直角三角形的三棱錐稱之為鱉臑，如圖為一個陽馬與一個鱉臑的組合體，已知
平面
，四邊形
為正方形，
，
，若鱉臑
的外接球的體積為
，則陽馬
的外接球的表面積等于______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
，
，…，
為1，2，…，10的一個排列，則滿足對任意正整數m，n，且
，都有
成立的不同排列的個數為（ ）
A.512B.256C.255D.64
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某校運動會男生組田徑綜合賽以選手三項運動的綜合積分高低決定排名．具體積分規則如表1所示，某代表隊四名男生的模擬成績如表2．
表1 田徑綜合賽項目及積分規則
項目 | 積分規則 |
| 以 |
跳高 | 以 |
擲實心球 | 以 |
表2 某隊模擬成績明細
姓名 | 100米跑（秒） | 跳高（米） | 擲實心球（米） |
甲 |
|
|
|
乙 |
|
|
|
丙 |
|
|
|
丁 |
|
|
|
根據模擬成績，該代表隊應選派參賽的隊員是：（ ）
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某城市為鼓勵人們綠色出行，乘坐地鐵，地鐵公司決定按照乘客經過地鐵站的數量實施分段優惠政策，不超過
站的地鐵票價如下表：
乘坐站數 |
|
|
|
票價（元） |
|
|
|
現有甲、乙兩位乘客同時從起點乘坐同一輛地鐵，已知他們乘坐地鐵都不超過
站.甲、乙乘坐不超過
站的概率分別為
， 
；甲、乙乘坐超過
站的概率分別為
， 
.
（1）求甲、乙兩人付費相同的概率；
（2）設甲、乙兩人所付費用之和為隨機變量
，求
的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
，橢圓
：
的離心率為
，
是橢圓的右焦點，直線
的斜率為
，
為坐標原點. 設過點
的動直線
與相交于
兩點.
（1）求的方程；
（2）是否存在這樣的直線，使得
的面積為
，若存在，求出的方程；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某產品自生產并投入市場以來，生產企業為確保產品質量，決定邀請第三方檢測機構對產品進行質量檢測，并依據質量指標
來衡量產品的質量.當
時，產品為優等品；當
時，產品為一等品；當
時，產品為二等品.第三方檢測機構在該產品中隨機抽取500件，繪制了這500件產品的質量指標的條形圖.用隨機抽取的500件產品作為樣本，估計該企業生產該產品的質量情況，并用頻率估計概率.
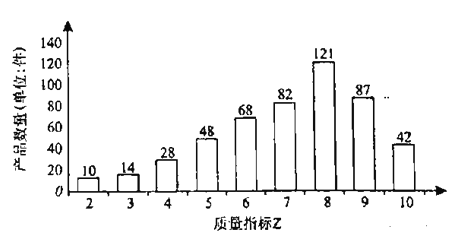
（1）從該企業生產的所有產品中隨機抽取1件，求該產品為優等品的概率；
（2）現某人決定購買80件該產品.已知每件成本1000元，購買前，邀請第三方檢測機構對要購買的80件產品進行抽樣檢測.買家、企業及第三方檢測機構就檢測方案達成以下協議：從80件產品中隨機抽出4件產品進行檢測，若檢測出3件或4件為優等品，則按每件1600元購買，否則按每件1500元購買，每件產品的檢測費用250元由企業承擔.記企業的收益為
元，求的分布列與數學期望；
（3）商場為推廣此款產品，現面向意向客戶推出“玩游戲，送大獎”活動.客戶可根據拋硬幣的結果，操控機器人在方格上行進，已知硬幣出現正、反面的概率都是
，方格圖上標有第0格、第1格、第2格、……、第50格.機器人開始在第0格，客戶每擲一次硬幣，機器人向前移動一次，若擲出正面，機器人向前移動一格（從
到
），若擲出反面，機器人向前移動兩格（從到
），直到機器人移到第49格（勝利大本營）或第50格（失敗大本營）時，游戲結束，若機器人停在“勝利大本營”，則可獲得優惠券.設機器人移到第
格的概率為
，試證明
是等比數列，并解釋此方案能否吸引顧客購買該款產品.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
