
【題目】設函數![]() (
(![]() 為常數).
為常數).
(1)當![]() 時,求曲線
時,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)若函數![]() 在
在![]() 內存在唯一極值點
內存在唯一極值點![]() ,求實數
,求實數![]() 的取值范圍,并判斷
的取值范圍,并判斷![]() 是
是![]() 在
在![]() 內的極大值點還是極小值點.
內的極大值點還是極小值點.
【答案】(1) ![]() (2)
(2) ![]() ,且
,且![]() 為函數
為函數![]() 的極小值點.
的極小值點.
【解析】
(1)先求出函數的導函數![]() ,再求出切線的斜率
,再求出切線的斜率![]() ,再由直線的點斜式方程求解即可;
,再由直線的點斜式方程求解即可;
(2)函數![]() 在
在![]() 內存在唯一極值點等價于方程
內存在唯一極值點等價于方程![]() 在
在![]() 內存在唯一解,再構造函數
內存在唯一解,再構造函數![]() ,求其值域,則可得
,求其值域,則可得![]() 的范圍,再利用導數確定
的范圍,再利用導數確定![]() 是極大值點或者極小值點.
是極大值點或者極小值點.
(1)當![]() 時,
時,![]() ,
,![]() ,
,
所求切線的斜率![]() ,又
,又![]() .
.
所以曲線![]() 在
在![]() 處的切線方程為:
處的切線方程為:![]() .
.
(2)![]() ,
,
又![]() ,則要使得
,則要使得![]() 在
在![]() 內存在唯一極值點,則
內存在唯一極值點,則![]() 在
在![]() 存在唯一變號零點,即方程
存在唯一變號零點,即方程![]() 在
在![]() 內存在唯一解,即
內存在唯一解,即![]() 與
與![]() 在
在![]() 范圍內有唯一交點,
范圍內有唯一交點,
設函數![]() ,則
,則![]() ,
,![]() 在
在![]() 單調遞減,又
單調遞減,又![]() ;當
;當![]() 時,
時,![]()
![]() 時,
時,![]() 與
與![]() 在
在![]() 范圍內有唯一交點,不妨設交點橫坐標為
范圍內有唯一交點,不妨設交點橫坐標為![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,則
,則![]() ,
,![]() 在
在![]() 為減函數;當
為減函數;當![]() 時,
時,![]() ,則
,則![]() ,
,![]() 在
在![]() 為增函數,即
為增函數,即![]() 為函數
為函數![]() 的極小值點,
的極小值點,
綜上所述:![]() ,且
,且![]() 為函數
為函數![]() 的極小值點.
的極小值點.


科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 為兩非零有理數列(即對任意的
為兩非零有理數列(即對任意的![]() ,
,![]() 均為有理數),
均為有理數),![]() 為一無理數列(即對任意的
為一無理數列(即對任意的![]() ,
,![]() 為無理數).
為無理數).
(1)已知![]() ,并且
,并且![]() 對任意的
對任意的![]() 恒成立,試求
恒成立,試求![]() 的通項公式.
的通項公式.
(2)若![]() 為有理數列,試證明:對任意的
為有理數列,試證明:對任意的![]() ,
,![]() 恒成立的充要條件為
恒成立的充要條件為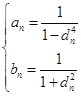 .
.
(3)已知![]() ,
,![]() ,對任意的
,對任意的![]() ,
,![]() 恒成立,試計算
恒成立,試計算![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
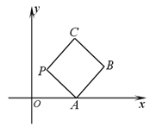
【題目】如圖所示,在平面直角坐標系![]() 上放置一個邊長為1的正方形
上放置一個邊長為1的正方形![]() ,此正方形
,此正方形![]() 沿
沿![]() 軸滾動(向左或向右均可),滾動開始時,點
軸滾動(向左或向右均可),滾動開始時,點![]() 位于原點處,設頂點
位于原點處,設頂點![]() 的縱坐標與橫坐標的函數關系式
的縱坐標與橫坐標的函數關系式![]() ,
,![]() ,該函數相鄰兩個零點之間的距離為
,該函數相鄰兩個零點之間的距離為![]() .
.
(1)寫出![]() 的值并求出頂點
的值并求出頂點![]() 到
到![]() 的最小運動路徑的長度
的最小運動路徑的長度![]() 的值;
的值;
(2)寫出函數![]() ,
,![]() ,
,![]() 的表達式;并研究該函數除周期外的基本性質(無需證明).
的表達式;并研究該函數除周期外的基本性質(無需證明).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】張軍自主創業,在網上經營一家干果店,銷售的干果中有松子、開心果、腰果、核桃,價格依次為120元/千克、80元/千克、70元/千克、40元千克,為增加銷量,張軍對這四種干果進行促銷:一次購買干果的總價達到150元,顧客就少付x(2x∈Z)元.每筆訂單顧客網上支付成功后,張軍會得到支付款的80%.
①若顧客一次購買松子和腰果各1千克,需要支付180元,則x=________;
②在促銷活動中,為保證張軍每筆訂單得到的金額均不低于促銷前總價的七折,則x的最大值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中無理數
,其中無理數![]() .
.
(Ⅰ)若函數![]() 有兩個極值點,求
有兩個極值點,求![]() 的取值范圍;
的取值范圍;
(Ⅱ)若函數![]() 的極值點有三個,最小的記為
的極值點有三個,最小的記為![]() ,最大的記為
,最大的記為![]() ,若
,若![]() 的最大值為
的最大值為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() (Ⅰ)求曲線
(Ⅰ)求曲線![]() 的直角坐標方程,并指出其表示何種曲線;(Ⅱ)設直線
的直角坐標方程,并指出其表示何種曲線;(Ⅱ)設直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,若點
兩點,若點![]() 的直角坐標為
的直角坐標為![]() ,試求當
,試求當![]() 時,
時,![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】清華大學自主招生考試題中要求考生從A,B,C三道題中任選一題作答,考試結束后,統計數據顯示共有600名學生參加測試,選擇A,B,C三題答卷數如下表:
題 | A | B | C |
答卷數 | 180 | 300 | 120 |
(Ⅰ)負責招生的教授為了解參加測試的學生答卷情況,現用分層抽樣的方法從600份答案中抽出若干份答卷,其中從選擇A題作答的答卷中抽出了3份,則應分別從選擇B,C題作答的答卷中各抽出多少份?
(Ⅱ)測試后的統計數據顯示,A題的答卷得優的有60份,若以頻率作為概率,在(Ⅰ)問中被抽出的選擇A題作答的答卷中,記其中得優的份數為![]() ,求
,求![]() 的分布列及其數學期望
的分布列及其數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com