
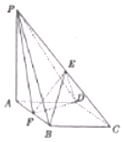
 如圖,在四棱錐P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥底面ABCD,E,F分別是PC,AB的中點.
如圖,在四棱錐P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥底面ABCD,E,F分別是PC,AB的中點.分析 (1)由PA⊥底面ABCD,可得PA⊥DF.再由底面ABCD是菱形,∠BAD=60°,可得△ABD是正三角形.進一步得到DF⊥AB.由線面垂直的判定可得DF⊥平面PAB.則DF⊥PB;
(2)由E是PC的中點,知點P到平面BDE的距離與點C到平面BDE的距離相等,然后利用等積法求得三棱錐P-BDE的體積.
解答 (1)證明:∵PA⊥底面ABCD,DF?平面ABCD,∴PA⊥DF.
∵底面ABCD是菱形,∠BAD=60°,∴△ABD是正三角形.
又∵F是AB的中點,∴DF⊥AB.
又∵PA∩AB=A,∴DF⊥平面PAB.
∵PB?平面PAB,∴DF⊥PB;
(2)解:∵E是PC的中點,∴點P到平面BDE的距離與點C到平面BDE的距離相等,
故VP-BDE=VC-BDE=VE-BCD,又${S}_{△BCD}=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$,
E到平面BCD的距離h=$\frac{1}{2}PA=\frac{3}{2}$,
∴${V}_{P-BDE}={V}_{E-BCD}=\frac{1}{3}×\sqrt{3}×\frac{3}{2}=\frac{\sqrt{3}}{2}$.
點評 本題考查直線與平面垂直的判定與性質,訓練了利用等積法求多面體的體積,是中檔題.


科目:高中數學 來源: 題型:解答題
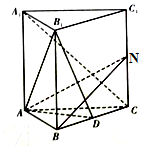 在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=$\sqrt{2}$,且D為BC中點.
在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=$\sqrt{2}$,且D為BC中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
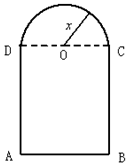 如圖,用長為12m的鐵絲彎成下部為矩形,上部為半圓形的框架窗戶,若半圓半徑
如圖,用長為12m的鐵絲彎成下部為矩形,上部為半圓形的框架窗戶,若半圓半徑查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 商品名稱 | A | B | C | D | E |
| 銷售額x(千萬元) | 3 | 5 | 6 | 7 | 9 |
| 利潤額y(百萬元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com