
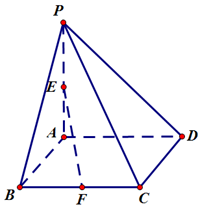
 如圖,在四棱錐P-ABCD中,PA⊥底面ABCD,底面ABCD為矩形,F是BC的中點,且PA=BC=2AB=2.
如圖,在四棱錐P-ABCD中,PA⊥底面ABCD,底面ABCD為矩形,F是BC的中點,且PA=BC=2AB=2.分析 (1)根據PA⊥底面ABCD可以推知CD⊥PA;
(2)當E是PA的中點時,EF∥平面PCD.如圖,取PD的中點G,連接EG、CG,構建平行四邊形EFCG,結合平行四邊形的對邊相互平行的性質和線面平行的性質證得結論EF∥平面PCD.
解答  證明:(1)又因為PA⊥底面ABCD,
證明:(1)又因為PA⊥底面ABCD,
CD?底面ABCD,所以CD⊥PA;
解:(2)當E是PA的中點時,EF∥平面PCD,
取PD的中點G,連接EG、CG,
又因為E、F分別是PA、BC的中點,底面ABCD為矩形,
所以EG∥AD∥FC且EG∥$\frac{1}{2}$AD∥FC,
所以四邊形EFCG是平行四邊形,
所以EF∥GC.
又因為EF?平面PCD,GC?平面PCD,
所以EF∥平面PCD.
點評 本題以底面為長方形、一條側棱垂直于底的四棱錐為載體,通過證明線面平行、垂直,著重考查了線面平行的判定定理、線面垂直的判定與性質等知識點,屬于中檔題.


科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,底面ABCD是邊長為2的正方形,側面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD
如圖,在四棱錐P-ABCD中,底面ABCD是邊長為2的正方形,側面PAD⊥底面ABCD,且PA=PD=$\frac{\sqrt{2}}{2}$AD查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\overrightarrow{a}$,$\overrightarrow{b}$方向相同 | |
| B. | $\overrightarrow{a}$,$\overrightarrow{b}$兩向量中至少有一個為零向量 | |
| C. | ?λ∈R,$\overrightarrow{b}$=λ$\overrightarrow{a}$ | |
| D. | 存在不全為零的實數λ1,λ2,λ1$\overrightarrow{a}$+λ2$\overrightarrow{b}$=$\overrightarrow{0}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com