
分析 (1)設雙曲線的標準方程為:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0).橢圓$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的焦點(±4,0),$\frac{c}{a}$=2,c2=a2+b2,聯立解得即可得出.
(2)依題意,可設橢圓C的方程為$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),則$\left\{\begin{array}{l}{\frac{4}{{a}^{2}}+\frac{9}{{b}^{2}}=1}\\{{a}^{2}-{b}^{2}=4}\end{array}\right.$,解出即可得出.
解答 解:(1)設雙曲線的標準方程為:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0).
橢圓$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的焦點(±4,0),$\frac{c}{a}$=2,c2=a2+b2,聯立解得a=2,b=2$\sqrt{3}$.
即所求雙曲線的方程$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}$=1.
(2)依題意,可設橢圓C的方程為$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
則$\left\{\begin{array}{l}{\frac{4}{{a}^{2}}+\frac{9}{{b}^{2}}=1}\\{{a}^{2}-{b}^{2}=4}\end{array}\right.$,
解得b2=12,a2=16,
所以橢圓C的方程為$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1.
點評 本題考查了橢圓與雙曲線的定義標準方程及其性質,考查了推理能力與計算能力,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
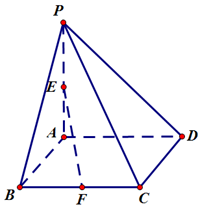 如圖,在四棱錐P-ABCD中,PA⊥底面ABCD,底面ABCD為矩形,F是BC的中點,且PA=BC=2AB=2.
如圖,在四棱錐P-ABCD中,PA⊥底面ABCD,底面ABCD為矩形,F是BC的中點,且PA=BC=2AB=2.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(0,\frac{1}{4})$ | B. | $(\frac{1}{4},1)$ | C. | (1,4) | D. | (4,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com