
分析 (1)函數f(x)>0在(0,+∞)上恒成立⇒m(x-2)<x2+x在(0,+∞)上恒成立,按x=2,x>2時,0<x<2分類求解;
(2)函數f(x)在(0,1)內有零點,⇒m(x-2)=x2+x在(0,1)上有解,m=$\frac{{x}^{2}+x}{x-2}=(x-2)+\frac{6}{x-2}+5$,在(0,1)上有解.
解答 解:(1)∵函數f(x)>0在(0,+∞)上恒成立⇒x2-(m-1)x+2m>0在(0,+∞)上恒成立,
⇒m(x-2)<x2+x在(0,+∞)上恒成立,
①當x=2時,m∈R,
②x>2時,m<$\frac{{x}^{2}+x}{x-2}=(x-2)+\frac{6}{x-2}+5$,∵$\frac{{x}^{2}+x}{x-2}=(x-2)+\frac{6}{x-2}+5$≥2$\sqrt{6}$+5,∵m<2$\sqrt{6}$+5;
③0<x<2時,m>$\frac{{x}^{2}+x}{x-2}=(x-2)+\frac{6}{x-2}+5$,∵(x-2)+$\frac{6}{x-2}$=-[(2-x)+$\frac{6}{2-x}$]<-5,
$\frac{{x}^{2}+x}{x-2}=(x-2)+\frac{6}{x-2}+5$<0,∴m≥0$\sqrt{6}+5$
綜上可知,m的取值范圍:0≤m<2$\sqrt{6}$+5.
(2)函數f(x)在(0,1)內有零點,⇒m(x-2)=x2+x在(0,1)上有解,m=$\frac{{x}^{2}+x}{x-2}=(x-2)+\frac{6}{x-2}+5$在(0,1)上有解.
令2-x=t,t∈(1,2),函數g(t)=t+$\frac{6}{t}+5$,t∈(1,2)時單調遞減,g(t)=∈(5,7)
x∈(0,1),$\frac{{x}^{2}+x}{x-2}=(x-2)+\frac{6}{x-2}+5$∈(-2,0).
故m的取值范圍:(-2,0).
點評 本題考查了恒成立問題的轉化思想,也考查了分類討論思想,函數的零點應用問題,是綜合題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
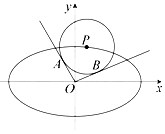 如圖,已知P(x0,y0)是橢圓C:$\frac{x^2}{a^2}+{y^2}$=1上一點,過原點的斜率分別為k1,k2的兩條直線與圓(x-x0)2+(y-y0)2=$\frac{4}{5}$分別相切于A,B兩點.
如圖,已知P(x0,y0)是橢圓C:$\frac{x^2}{a^2}+{y^2}$=1上一點,過原點的斜率分別為k1,k2的兩條直線與圓(x-x0)2+(y-y0)2=$\frac{4}{5}$分別相切于A,B兩點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
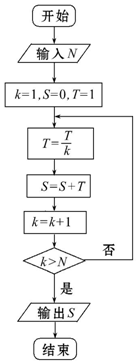
| A. | $1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{10}$ | B. | 1+$\frac{1}{1×2}$+$\frac{1}{1×2×3}$+…+$\frac{1}{1×2×…×10}$ | ||
| C. | $1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{11}$ | D. | 1+$\frac{1}{1×2}$+$\frac{1}{1×2×3}$+…+$\frac{1}{1×2×…×11}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com