
分析 (1)利用二倍角公式以及兩角和與差的三角函數化簡函數的解析式,然后求解它的振幅、周期和初相;
(2)利用正弦函數的最值,求解函數的最值即可.
(3)利用正弦函數的單調性求解函數的單調區間即可.
解答 解:y=$\frac{1}{2}$cos2x+$\frac{{\sqrt{3}}}{2}$sinxcosx+1=$\frac{1}{4}$cos2x+$\frac{{\sqrt{3}}}{4}$sin2x+$\frac{5}{4}$
=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)+$\frac{5}{4}$…(4分)
(1)函數的振幅為A=$\frac{1}{2}$,周期為T=$\frac{2π}{2}$=π,初相為φ=$\frac{π}{6}$…(6分)
(2)函數的最大值是$\frac{1}{2}$+$\frac{5}{4}$=$\frac{7}{4}$,此時2x+$\frac{π}{6}$=$\frac{π}{2}$+2kπ,x=$\frac{π}{6}$+kπ,k∈Z…(8分)
函數的最小值是$-\frac{1}{2}$+$\frac{5}{4}$=$\frac{3}{4}$,此時2x+$\frac{π}{6}$=$-\frac{π}{2}$+2kπ,x=$-\frac{π}{3}$+kπ,k∈Z…(10分)
(3)$-\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,∴$-\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,k∈Z…(12分)
∴函數的單調遞增區間為[$-\frac{π}{3}$+kπ,$\frac{π}{6}$+kπ],(k∈Z)…(14分)
點評 本題考查兩角和與差的三角函數,三角函數的振幅、周期、相位以及函數的最值的求法,單調性的判斷,是中檔題.


 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:高中數學 來源: 題型:解答題
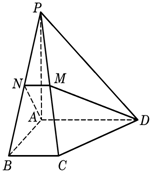 如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M、N分別為PC、PB的中點.
如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M、N分別為PC、PB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
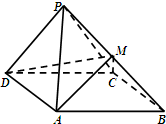 如圖,四棱錐P-ABCD中,側面PDC是邊長為2的正三角形,底面ABCD是菱形,∠ADC=60°,點P在底面ABCD上的射影為△ACD的重心,點M為線段PB上的點.
如圖,四棱錐P-ABCD中,側面PDC是邊長為2的正三角形,底面ABCD是菱形,∠ADC=60°,點P在底面ABCD上的射影為△ACD的重心,點M為線段PB上的點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖四邊形ABCD是邊長為2的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且NB=MD=2,E為BC的中點.
如圖四邊形ABCD是邊長為2的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且NB=MD=2,E為BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
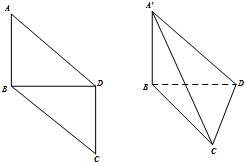 如圖,在平行四邊形ABCD中,AB=BD=DC=1,AD=BC=$\sqrt{2}$,將平行四邊形ABCD沿對角線BD折成三棱錐A′-BCD,使平面A′BD⊥平面BCD,在下列結論中:
如圖,在平行四邊形ABCD中,AB=BD=DC=1,AD=BC=$\sqrt{2}$,將平行四邊形ABCD沿對角線BD折成三棱錐A′-BCD,使平面A′BD⊥平面BCD,在下列結論中:查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com