
分析 由題意可知,兩邊取倒數(shù)可得:則$\frac{1}{(n+1){a}_{n+1}}$-$\frac{1}{n{a}_{n}}$=1,又$\frac{1}{1•{a}_{1}}$=2,
數(shù)列{$\frac{1}{n{a}_{n}}$}是以2為首項(xiàng),1為公差的等差數(shù)列,利用等差數(shù)列的通項(xiàng)公式即可得出an.不等式$\frac{3}{n^2}+\frac{1}{n}+t{a_n}≥0$化為:t≥-(n+$\frac{3}{n}$+4).再利用基本不等式的性質(zhì)即可得出實(shí)數(shù)t的取值范圍.
解答 解:∵an+1=$\frac{n{a}_{n}}{(n+1)(n{a}_{n}+1)}$(n∈N*),
∴$\frac{1}{{a}_{n+1}}$=$\frac{(n+1)n{a}_{n}+(n+1)}{n{a}_{n}}$=(n+1)+$\frac{n+1}{n{a}_{n}}$,
即$\frac{1}{(n+1){a}_{n+1}}$-$\frac{1}{n{a}_{n}}$=1,又$\frac{1}{1•{a}_{1}}$=2,
∴數(shù)列{$\frac{1}{n{a}_{n}}$}是以2為首項(xiàng),1為公差的等差數(shù)列,
∴$\frac{1}{n{a}_{n}}$=2+(n-1)=n+1,
∴an=$\frac{1}{n(n+1)}$.
∵不等式$\frac{3}{n^2}+\frac{1}{n}+t{a_n}≥0$化為:t≥-(n+$\frac{3}{n}$+4).
∵n+$\frac{3}{n}$+4≥2$\sqrt{n×\frac{3}{n}}$+4=4+2$\sqrt{3}$,當(dāng)且僅當(dāng)n=$\frac{3}{n}$時(shí)取等號,
由n∈N*,則當(dāng)n=2時(shí),n+$\frac{3}{n}$+4取最小,最小值為$\frac{15}{2}$
∴t≥-$\frac{15}{2}$,
故答案為:[-$\frac{15}{2}$,+∞).
點(diǎn)評 本題考查了等差數(shù)列的通項(xiàng)公式、基本不等式的性質(zhì),考查了推理能力與計(jì)算能力,屬于中檔題.


 黃岡小狀元同步計(jì)算天天練系列答案
黃岡小狀元同步計(jì)算天天練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | y=sin2x | B. | $y=sin(\frac{x}{2}-\frac{π}{6})$ | C. | $y=-cos\frac{x}{2}$ | D. | $y=sin(2x-\frac{π}{6})$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
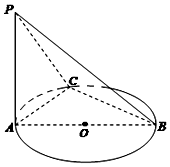 如圖,AB是⊙O的直徑,PA垂直于⊙O所在平面,C是圓周上不同于A,B兩點(diǎn)的任意一點(diǎn),且AB=2,$PA=BC=\sqrt{3}$,則直線PC與底面ABC所成角的大小為( )
如圖,AB是⊙O的直徑,PA垂直于⊙O所在平面,C是圓周上不同于A,B兩點(diǎn)的任意一點(diǎn),且AB=2,$PA=BC=\sqrt{3}$,則直線PC與底面ABC所成角的大小為( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $({\sqrt{5},2\sqrt{5}})$ | B. | $({2\sqrt{5},5})$ | C. | $({\sqrt{5},5})$ | D. | $({2,\sqrt{5}})$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com