Question

1．定義區間（a，d），[a，d），（a，d]，[a，d]的長度為d-a（d＞a），已知a＞b，則滿足$\frac{1}{x-a}+\frac{1}{x-b}≥1$的x構成的區間的長度之和為2．

Answer 1

分析 根據不等式進行化簡，求出不等式對應的解集，根據區間長度的定義進行求解即可．

解答 解：∵$\frac{1}{x-a}+\frac{1}{x-b}≥1$，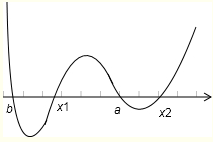
∴$\frac{2x-（a+b）}{（x-a）（x-b）}$≥1，
即$\frac{2x-（a+b）}{（x-a）（x-b）}$-1≥0，則$\frac{{x}^{2}-（2+a+b）x+ab+a+b}{（x-a）（x-b）}$≤0，
設x²-（2+a+b）x+ab+a+b=0的根為x₁和x₂．
則有求根公式得x₁=$\frac{a+b+2-\sqrt{（a-b）^{2}+4}}{2}$∈（a，b），
x₂=$\frac{a+b+2+\sqrt{（a-b）^{2}+4}}{2}$＞a，
x₁+x₂═2+a+b，
則由穿根法得不等式的解集為[b，x₁]∪[a-x₂]，
則構成的區間的長度之和x₁-b+x₂-a=x₁-x₂-a-b=2+a+b-a-b=2，
故答案為：2

點評 本題主要考查區間長度的定義，利用穿根法求出不等式的解集是解決本題的關鍵．