
分析 (1)確定雙曲線的焦點在x軸上,設其方程為x2-y2=a2,代入$P(3,\sqrt{5})$得a2=4,即可求雙曲線C的方程;
(2)求出雙曲線的漸近線方程,求出直線與另一條漸近線的交點,然后求出三角形的面積.
解答 解:(1)設雙曲線的實軸長為2a,虛軸長為2b,則$\frac{b}{a}=\frac{{\sqrt{{c^2}-{a^2}}}}{a}=\sqrt{{e^2}-1}=1$--(2分)
∴a=b,故雙曲線的漸近線方程為y=±x,----------(4分)
將x=3代入y=x得$y=3>\sqrt{5}$,
故雙曲線的焦點在x軸上,--------(6分)
設其方程為x2-y2=a2,代入$P(3,\sqrt{5})$得a2=4,
故所求雙曲線方程為x2-y2=4.----------(8分)
(2)雙曲線x2-y2=4的左頂點A(-2,0),漸近線方程為y=±x
過點A與漸近線y=x平行的直線方程為y=x+2,--------(10分)
它與雙曲線的另一漸近線y=-x交于M(-1,1)
∴所求三角形的面積為.$S=\frac{1}{2}|{OA}|{y_M}=\frac{1}{2}×2×1=1$---------------(12分)
點評 本題考查直線與圓錐曲線的綜合問題,考查分析問題解決問題的能力,考查計算能力.


科目:高中數學 來源: 題型:選擇題
| A. | $(-\frac{π}{8},0)$ | B. | $(-\frac{π}{4},0)$ | C. | $(-\frac{π}{8},1)$ | D. | $(-\frac{π}{4},1)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(3+4\sqrt{2},+∞)$ | B. | $(2\sqrt{2}-1,+∞)$ | C. | $(0,2\sqrt{2}-1)$ | D. | $(0,3+4\sqrt{2})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{5+2\sqrt{6}}}{2}$ | B. | $5+2\sqrt{6}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
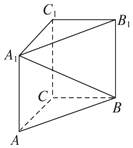 如圖,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,則異面直線A1B與AC所成角的余弦值是( )
如圖,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,則異面直線A1B與AC所成角的余弦值是( )| A. | $\frac{{\sqrt{6}}}{5}$ | B. | $\frac{{\sqrt{6}}}{4}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{3\sqrt{13}}{26}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com