
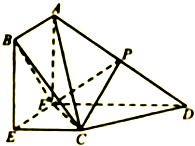
 如圖,四邊形ABEF為矩形,四邊形CEFD為直角梯形,CE∥DF,EF⊥FD,平面ABEF⊥平面CEFD,P為AD的中點,且AB=EC=$\frac{1}{2}$FD.
如圖,四邊形ABEF為矩形,四邊形CEFD為直角梯形,CE∥DF,EF⊥FD,平面ABEF⊥平面CEFD,P為AD的中點,且AB=EC=$\frac{1}{2}$FD.分析 (1)通過證明AF⊥CD,CD⊥FC.即可證明CD⊥平面ACF.
(2)利用空間直角坐標系,通過求解平面的法向量,利用向量的數量積求解即可.
解答 (1)證明:∵AF⊥EF,平面ABEF⊥平面CEFD,平面ABEF∩平面CEFD=EF,
∴AF⊥平面CEFD,從而AF⊥CD.
設Q為DF的中點,連接CQ.
∵四邊形CEFD為直角梯形,EC=$\frac{1}{2}$FD=FQ,EC=AB=EF,
∴四邊形CEFQ為正方形,△CQD為等腰直角三角形.
∴∠FCD=90°,即CD⊥FC.
又AF∩CF=F,∴CD⊥平面ACF…(6分)
(2)解:以F為坐標原點,FE,FD,FA所在直線分別為x,y,z軸建立如圖所示的空間直角 坐標系,設AB=1,則BE=2,FD=2.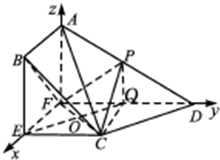
∴F(0,0,0),C(1,1,0),B(1,0,2),D(0,2,0),A(0,0,2),P(0,1,1),
故$\overrightarrow{FC}$=(1,1,0),$\overrightarrow{PB}$=(1,0,2),$\overrightarrow{FP}$=(0,1,1),設平面SFC的一個法向量$\overrightarrow{{n}_{1}}$=(x1,y1,z1),則$\overrightarrow{{n}_{1}}•\overrightarrow{FC}=0$,$\overrightarrow{{n}_{1}}•\overrightarrow{FB}=0$
∴$\left\{\begin{array}{l}{{x}_{1}+{y}_{1}=0}\\{{x}_{1}+2{z}_{1}=0}\end{array}\right.$,令z1=1,則$\overrightarrow{{n}_{1}}$=(-2,2,1).
同理可得,平面FCP的一個法向量$\overrightarrow{{n}_{2}}$=(1,-1,1).
∴cos$<\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}>$=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=-$\frac{\sqrt{3}}{3}$,由圖可知,二面角B-FC-P的余弦值為:$-\frac{\sqrt{3}}{3}$…(12分)
點評 本題考查二面角的平面鏡的求法,直線與平面垂直的判定定理的應用,考查空間想象能力以及計算能力.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
| 損壞餐椅數 | 未損壞餐椅數 | 總 計 | |
| 學習雷鋒精神前 | 50 | 150 | 200 |
| 學習雷鋒精神后 | 30 | 170 | 200 |
| 總 計 | 80 | 320 | 400 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com