【題目】如圖所示，
、
是兩個垃圾中轉站，在的正東方向
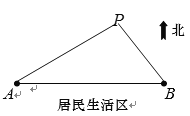
千米處，
的南面為居民生活區．為了妥善處理生活垃圾，政府決定在的北面建一個垃圾發電廠
．垃圾發電廠的選址擬滿足以下兩個要求（、、可看成三個點）：①垃圾發電廠到兩個垃圾中轉站的距離與它們每天集中的生活垃圾量成反比，比例系數相同；②垃圾發電廠應盡量遠離居民區（這里參考的指標是點到直線的距離要盡可能大）．現估測得、兩個中轉站每天集中的生活垃圾量分別約為
噸和
噸．設
．
（1）求
（用
的表達式表示）；
（2）垃圾發電廠該如何選址才能同時滿足上述要求？
100分闖關期末沖刺系列答案科目：高中數學 來源： 題型：
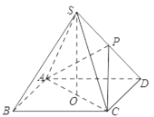
【題目】如圖，在四棱錐
中，已知四邊形
是邊長為
的正方形，點
在底面上的射影為底面的中心點
，點
在棱
上，且
的面積為1．
（1）若點是的中點，求證：平面
平面
；
（2）在棱上是否存在一點使得二面角
的余弦值為
？若存在，求出點的位置；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】《算法統宗》全稱《新編直指算法統宗》，是屮國古代數學名著，程大位著.書中有如下問題：“今有五人均銀四十兩，甲得十兩四錢，戊得五兩六錢.問：次第均之，乙丙丁各該若干？”意思是：有5人分40兩銀子，甲分10兩4錢，戊分5兩6錢，且相鄰兩項差相等，則乙丙丁各分幾兩幾錢？（注：1兩等于10錢）（ ）
A.乙分8兩，丙分8兩，丁分8兩B.乙分8兩2錢，丙分8兩，丁分7兩8錢
C.乙分9兩2錢，丙分8兩，丁分6兩8錢D.乙分9兩，丙分8兩，丁分7兩
查看答案和解析>>
科目：高中數學 來源： 題型：
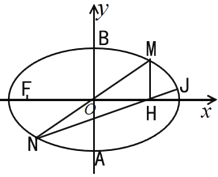
【題目】已知橢圓
的左焦點為F，短軸的兩個端點分別為A、B，且
，
為等邊三角形.
（1）求橢圓C的方程；
（2）如圖，點M在橢圓C上且位于第一象限內，它關于坐標原點O的對稱點為N；過點M作x軸的垂線，垂足為H，直線
與橢圓C交于另一點J，若
，試求以線段
為直徑的圓的方程；
（3）已知
是過點A的兩條互相垂直的直線，直線
與圓
相交于
兩點，直線
與橢圓C交于另一點R；求
面積取最大值時，直線的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列
滿足
，其中A，B是兩個確定的實數，
（1）若
，求的前n項和；
（2）證明：不是等比數列；
（3）若
，數列中除去開始的兩項外，是否還有相等的兩項，并證明你的結論.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐
中，底面
為梯形， 
底面
， 
， 
， 
， 
．
（1）求證：平面
平面
；
（2）設
為
上的一點，滿足
，若直線
與平面
所成角的正切值為
，求二面角
的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知兩個無窮數列
分別滿足
，
，
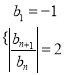其中
，設數列的前
項和分別為
，
（1）若數列都為遞增數列，求數列的通項公式；
（2）若數列
滿足：存在唯一的正整數
（
），使得
，稱數列為“墜點數列”
①若數列
為“5墜點數列”，求
；
②若數列為“
墜點數列”，數列
為“
墜點數列”，是否存在正整數
，使得
，若存在，求的最大值；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知四棱錐
的底面為正方形，且該四棱錐的每條棱長均為
，設BC，CD的中點分別為E，F，點G在線段PA上，如圖.
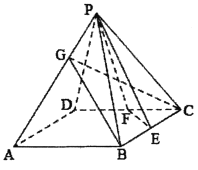
（1）證明：
；
（2）當
平面PEF時，求直線GC和平面PEF所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
