
【題目】已知橢圓![]() 的左焦點為F,短軸的兩個端點分別為A、B,且
的左焦點為F,短軸的兩個端點分別為A、B,且![]() ,
,![]() 為等邊三角形.
為等邊三角形.
(1)求橢圓C的方程;
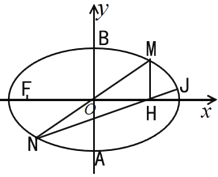
(2)如圖,點M在橢圓C上且位于第一象限內,它關于坐標原點O的對稱點為N;過點M作x軸的垂線,垂足為H,直線![]() 與橢圓C交于另一點J,若
與橢圓C交于另一點J,若![]() ,試求以線段
,試求以線段![]() 為直徑的圓的方程;
為直徑的圓的方程;
(3)已知![]() 是過點A的兩條互相垂直的直線,直線
是過點A的兩條互相垂直的直線,直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,直線
兩點,直線![]() 與橢圓C交于另一點R;求
與橢圓C交于另一點R;求![]() 面積取最大值時,直線
面積取最大值時,直線![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() .(也可寫成
.(也可寫成![]() .)
.)
【解析】
(1)由橢圓左焦點為F,短軸的兩個端點分別為A、B,且![]() ,
,![]() 為等邊三角形,列出方程組,求出a,b,由此能求出橢圓C的方程.
為等邊三角形,列出方程組,求出a,b,由此能求出橢圓C的方程.
(2)設![]() ,則由條件,知
,則由條件,知![]() ,
,![]() ,且
,且![]() ,
,![]() .推導出
.推導出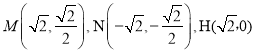 ,進而求得直線NH的方程:
,進而求得直線NH的方程:![]() .由
.由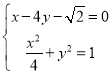 求得
求得![]() .再求出線段
.再求出線段![]() 的中點坐標,由此能求出以線段
的中點坐標,由此能求出以線段![]() 為直徑的圓的方程.
為直徑的圓的方程.
(3)當直線![]() 的斜率為0時,
的斜率為0時,![]() .當直線
.當直線![]() 的斜率存在且不為0時,設其方程為
的斜率存在且不為0時,設其方程為![]() ,利用點到直線距離公式、弦長公式、直線垂直、三角形面積公式,結合已知條件能求出結果.
,利用點到直線距離公式、弦長公式、直線垂直、三角形面積公式,結合已知條件能求出結果.
(1)∵橢圓![]() 的左焦點為F,短軸的兩個端點分別為A、B
的左焦點為F,短軸的兩個端點分別為A、B
且![]() ,
,![]() 為等邊三角形.
為等邊三角形.
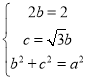 ,解得
,解得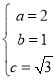 ,∴橢圓C的方程為
,∴橢圓C的方程為(2)設![]() ,則由條件,知
,則由條件,知![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
從而![]() .
.
于是由![]() 及
及![]() ,得
,得![]() .
.
再由點M在橢圓C上,得![]() ,求得
,求得![]() .
.
所以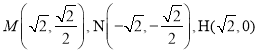 ,
,
進而求得直線NH的方程:![]() .
.
由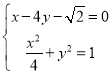 求得
求得![]() .
.
進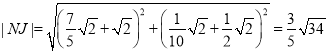 ,
,
線段![]() 的中點坐標為
的中點坐標為![]() .
.
∴以線段![]() 為直徑的圓的方程為:
為直徑的圓的方程為:![]() .
.
(3)當直線![]() 的斜率不存在時,直線
的斜率不存在時,直線![]() 與橢圓C相切于點A,不合題意,
與橢圓C相切于點A,不合題意,
當直線![]() 的斜率為0時,由題意得
的斜率為0時,由題意得![]() .
.
當直線![]() 的斜率存在且不為0時,設其方程為
的斜率存在且不為0時,設其方程為![]() ,
,
則點O到直線![]() 的距離為
的距離為![]() ,從而由幾何意義,得
,從而由幾何意義,得![]() ,
,
由于![]() ,故直線
,故直線![]() 的方程為
的方程為![]() ,由題意得它與橢圓C的交點R的坐標為
,由題意得它與橢圓C的交點R的坐標為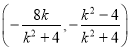 ,
,
于是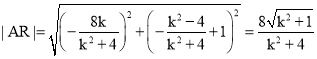 .
.
故![]() ,
,
令![]() ,則
,則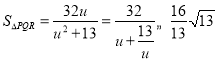 ,
,
當且僅當![]() 即
即![]() 時,上式取等號.
時,上式取等號.
∵![]() ,故當
,故當![]() 時,
時,![]() ,
,
此時直線![]() 的方程為:
的方程為:![]() .(也可寫成
.(也可寫成![]() .)
.)


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源: 題型:
【題目】如圖,在底面是菱形的四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 在
在![]() 上,且
上,且![]() .
.
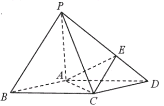
(1)證明:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一點
上是否存在一點![]() ,使三棱錐
,使三棱錐![]() 是正三棱錐?證明你的結論.
是正三棱錐?證明你的結論.
(3)求以![]() 為棱,
為棱,![]() 與
與![]() 為面的二面角
為面的二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某書店剛剛上市了《中國古代數學史》,銷售前該書店擬定了5種單價進行試銷,每本單價(![]() 元)試銷l天,得到如表單價
元)試銷l天,得到如表單價![]() (元)與銷量
(元)與銷量![]() (冊)數據:
(冊)數據:
單價 |
|
|
|
|
|
銷量 |
|
|
|
|
|
(1)已知銷量![]() 與單價
與單價![]() 具有線性相關關系,求
具有線性相關關系,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)若該書每本的成本為![]() 元,要使得售賣時利潤最大,請利用所求的線性相關關系確定單價應該定為多少元?(結果保留到整數)
元,要使得售賣時利潤最大,請利用所求的線性相關關系確定單價應該定為多少元?(結果保留到整數)
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: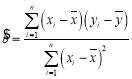
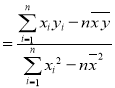 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l1:kx-y+4=0與直線l2:x+ky-3=0相交于點P,則當實數k變化時,點P到直線4x-3y+10=0的距離的最大值為( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的奇函數,當
上的奇函數,當![]() 時,
時,![]() ,給出下列命題:
,給出下列命題:
①當![]() 時,
時,![]() ②函數
②函數![]() 有3個零點
有3個零點
③![]() 的解集為
的解集為![]() ④
④![]() ,都有
,都有![]()
其中正確命題的個數是( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是中國古代第一部數學專著,全書總結了戰國、秦、漢時期的數學成就。“更相減損術”便出自其中,原文記載如下:“可半者半之,不可半者,副置分母、子之數,以少減多,更相減損,求其等也。”其核心思想編譯成如示框圖,若輸入的![]() ,
,![]() 分別為45,63,則輸出的
分別為45,63,則輸出的![]() 為( )
為( )
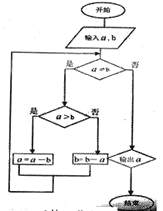
A. 2B. 3C. 5D. 9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代有著輝煌的數學研究成果,其中的《周髀算經》、《九章算術》、《海島算經》、《孫子算經》、《緝古算經》,有豐富多彩的內容,是了解我國古代數學的重要文獻,這5部專著中有3部產生于漢、魏、晉、南北朝時期,某中學擬從這5部專著中選擇2部作為“數學文化”校本課程學習內容,則所選2部專著中至少有一部是漢、魏、晉、南北朝時期專著的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com