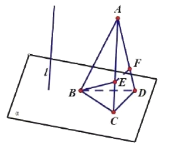
【題目】正四面體
中，
在平面
內，點
在線段
上，
，
是平面的垂線，在該四面體繞
旋轉的過程中，直線
與所成角為
，則
的最小值是（ ）
A.
B.
C.
D.
科目：高中數學 來源： 題型：
【題目】為了鼓勵職員工作熱情，某公司對每位職員一年來的工作業績按月進行考評打分；年終按照職員的月平均值評選公司最佳職員并給予相應獎勵.已知職員
一年來的工作業績分數的莖葉圖如圖所示：
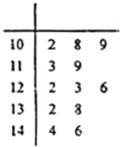
（1）根據職員的業績莖葉圖求出他這一年的工作業績的中位數和平均數；
（2）由于職員的業績高，被公司評為年度最佳職員，在公司年會上通過抽獎形式領取獎金.公司準備了六張卡片，其中一張卡片上標注獎金為6千元，兩張卡片的獎金為4千元，另外三張的獎金為2千元.規則是：獲獎職員需要從六張卡片中隨機抽出兩張，這兩張卡片上的金額數之和作為獎金數.求職員獲得獎金6千元的概率；并說明獲得獎金6千元和8千元哪個可能性較大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2017年11月河南省三門峽市成功入圍“十佳魅力中國城市”，吸引了大批投資商的目光，一些投資商積極準備投入到“魅力城市”的建設之中.某投資公司準備在2018年年初將四百萬元投資到三門峽下列兩個項目中的一個之中.
項目一：天坑院是黃土高原地域獨具特色的民居形式，是人類“穴居”發展史演變的實物見證.現準備投資建設20個天坑院，每個天坑院投資0.2百萬元，假設每個天坑院是否盈利是相互獨立的，據市場調研，到2020年底每個天坑院盈利的概率為
，若盈利則盈利投資額的40%，否則盈利額為0.
項目二：天鵝湖國家濕地公園是一處融生態、文化和人文地理于一體的自然山水景區.據市場調研，投資到該項目上，到2020年底可能盈利投資額的50%，也可能虧損投資額的30%，且這兩種情況發生的概率分別為p和
.
（1）若投資項目一，記
為盈利的天坑院的個數，求
（用p表示）；
（2）若投資項目二，記投資項目二的盈利為
百萬元，求
（用p表示）；
（3）在（1）（2）兩個條件下，針對以上兩個投資項目，請你為投資公司選擇一個項目，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系中，曲線
的參數方程為
（
為參數），以
為極點，
軸正半軸為極軸建立極坐標系，直線
的極坐標方程為
.
（1）將曲線上各點的縱坐標伸長為原來的
倍（橫坐標不變）得到曲線
，求的參數方程；
（2）若
，
分別是直線與曲線上的動點，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，當
，
時，
的值域為
，
，當
，時，的值域為
，
，依此類推，一般地，當
，
時，的值域為
，
，其中
、
為常數，且
，
．
（1）若
，求數列
，
的通項公式；
（2）若
，問是否存在常數
，使得數列滿足
？若存在，求的值；若不存在，請說明理由；
（3）若
，設數列，的前
項和分別為
，
，求
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，墻上有一壁畫，最高點
離地面4米，最低點
離地面2米，觀察者從距離墻
米，離地面高
米的
處觀賞該壁畫，設觀賞視角
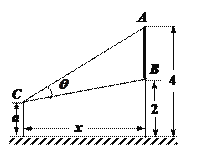
（1）若
問：觀察者離墻多遠時，視角
最大？
（2）若
當
變化時，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖數表：
每一行都是首項為1的等差數列，第
行的公差為
，且每一列也是等差數列，設第行的第
項為
.
（1）證明：
成等差數列，并用
表示（
）；
（2）當
時，將數列
分組如下：（
），（
），（
），…（每組數的個數構成等差數列）. 設前組中所有數之和為
，求數列
的前
項和
；
（3）在（2）的條件下，設
是不超過20的正整數，當
時，求使得不等式
恒成立的所有的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
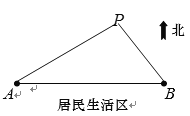
【題目】如圖所示，
、
是兩個垃圾中轉站，在的正東方向
千米處，
的南面為居民生活區．為了妥善處理生活垃圾，政府決定在的北面建一個垃圾發電廠
．垃圾發電廠的選址擬滿足以下兩個要求（、、可看成三個點）：①垃圾發電廠到兩個垃圾中轉站的距離與它們每天集中的生活垃圾量成反比，比例系數相同；②垃圾發電廠應盡量遠離居民區（這里參考的指標是點到直線的距離要盡可能大）．現估測得、兩個中轉站每天集中的生活垃圾量分別約為
噸和
噸．設
．
（1）求
（用
的表達式表示）；
（2）垃圾發電廠該如何選址才能同時滿足上述要求？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
