
【題目】已知兩個無窮數列![]() 分別滿足
分別滿足![]() ,
,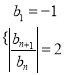 ,
,
其中![]() ,設數列
,設數列![]() 的前
的前![]() 項和分別為
項和分別為![]() ,
,
(1)若數列![]() 都為遞增數列,求數列
都為遞增數列,求數列![]() 的通項公式;
的通項公式;
(2)若數列![]() 滿足:存在唯一的正整數
滿足:存在唯一的正整數![]() (
(![]() ),使得
),使得![]() ,稱數列
,稱數列![]() 為“
為“![]() 墜點數列”
墜點數列”
①若數列![]() 為“5墜點數列”,求
為“5墜點數列”,求![]() ;
;
②若數列![]() 為“
為“![]() 墜點數列”,數列
墜點數列”,數列![]() 為“
為“![]() 墜點數列”,是否存在正整數
墜點數列”,是否存在正整數![]() ,使得
,使得![]() ,若存在,求
,若存在,求![]() 的最大值;若不存在,說明理由.
的最大值;若不存在,說明理由.
【答案】(1)![]() ,
,![]() (2)①
(2)①![]() ②
②![]()
【解析】
(1)∵數列![]() 都為遞增數列,
都為遞增數列,
∴由遞推式可得![]() ,
,![]() ,
,
則數列![]() 為等差數列,數列
為等差數列,數列![]() 從第二項起構成等比數列.
從第二項起構成等比數列.
∴![]() ;
;
(2)①∵數列![]() 滿足:存在唯一的正整數k=5,使得
滿足:存在唯一的正整數k=5,使得![]() ,且
,且![]() ,
,
∴數列![]() 必為1,3,5,7,5,7,9,11,…,即前4項為首項為1,公差為2的等差數列,從第5項開始為首項5,公差為2的等差數列,
必為1,3,5,7,5,7,9,11,…,即前4項為首項為1,公差為2的等差數列,從第5項開始為首項5,公差為2的等差數列,
故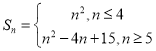 ;
;
②∵![]() ,即
,即![]() ,∴
,∴![]() ,而數列
,而數列![]() 為“
為“![]() 墜點數列”且
墜點數列”且![]() ,數列
,數列![]() 中有且只有兩個負項.假設存在正整數
中有且只有兩個負項.假設存在正整數![]() ,使得
,使得![]() ,顯然
,顯然![]() ,且
,且![]()
![]() 中各項均為奇數,∴
中各項均為奇數,∴![]() 必為偶數.
必為偶數. ![]() .
.
ⅰ.當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,故不存在
,故不存在![]() ,使得
,使得![]() 成立.
成立.
ⅱ.當![]() 時,
時,![]() ,顯然不存在
,顯然不存在![]() ,使得
,使得![]() 成立.
成立.
ⅲ.當![]() 時,
時,![]() ,當
,當![]() 時,才存在
時,才存在![]() ,使得
,使得![]() 成立.所以
成立.所以![]() .當
.當![]() 時,
時,![]() ,構造
,構造![]() 為1,3,1,3,5,7,9,…,
為1,3,1,3,5,7,9,…,![]() 為-1,2,4,8,-16,32,…,此時
為-1,2,4,8,-16,32,…,此時![]() ,所以
,所以![]() 的最大值為6.
的最大值為6.


科目:高中數學 來源: 題型:
【題目】已知![]() 為定義在實數集
為定義在實數集![]() 上的函數,把方程
上的函數,把方程![]() 稱為函數
稱為函數![]() 的特征方程,特征方程的兩個實根
的特征方程,特征方程的兩個實根![]() 、
、![]() (
(![]() ),稱為
),稱為![]() 的特征根.
的特征根.
(1)討論函數![]() 的奇偶性,并說明理由;
的奇偶性,并說明理由;
(2)已知![]() 為給定實數,求
為給定實數,求![]() 的表達式;
的表達式;
(3)把函數![]() ,
,![]() 的最大值記作
的最大值記作![]() ,最小值記作
,最小值記作![]() ,研究函數
,研究函數![]() ,
,![]() 的單調性,令
的單調性,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 和直線
和直線![]() :
: ![]() ,橢圓的離心率
,橢圓的離心率![]() ,坐標原點到直線
,坐標原點到直線![]() 的距離為
的距離為![]() .
.
(Ⅰ)求橢圓的方程;
(Ⅱ)已知定點![]() ,若直線
,若直線![]() 過點
過點![]() 且與橢圓相交于
且與橢圓相交于![]() 兩點,試判斷是否存在直線
兩點,試判斷是否存在直線![]() ,使以
,使以![]() 為直徑的圓過點
為直徑的圓過點![]() ?若存在,求出直線
?若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義在區間![]() 的函數
的函數![]() ,定義:
,定義:![]() (
(![]() ),
),![]() (
(![]() ),其中,
),其中,![]() 表示函數
表示函數![]() 在
在![]() 上的最小值,
上的最小值,![]() 表示函數
表示函數![]() 在
在![]() 上的最大值.
上的最大值.
(1)若![]() ,
,![]() ,試寫出
,試寫出![]() 、
、![]() 的表達式;
的表達式;
(2)設![]() 且
且![]() ,函數
,函數![]() ,
,![]() ,如果
,如果![]() 與
與![]() 恰好為同一函數,求
恰好為同一函數,求![]() 的取值范圍.
的取值范圍.
(3)若存在最小正整數![]() ,使得
,使得![]() 對任意的
對任意的![]() 成立,則稱函數
成立,則稱函數![]() 為
為![]() 上的“
上的“![]() 階收縮函數”,已知函數
階收縮函數”,已知函數![]() ,
,![]() ,試判斷
,試判斷![]() 是否為
是否為![]() 上的“
上的“![]() 階收縮函數”,如果是,求出對應的
階收縮函數”,如果是,求出對應的![]() ,如果不是,請說明理由.
,如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某創業投資公司投資開發某種新能源產品,估計能獲得10萬元到100萬元的投資收益,現準備制定一個對科研課題組的獎勵方案:①獎金![]() (單位:萬元)隨投資收益
(單位:萬元)隨投資收益![]() (單位:萬元)的增加而增加;②獎金不超過9萬元;③獎金不超過投資收益的20%.
(單位:萬元)的增加而增加;②獎金不超過9萬元;③獎金不超過投資收益的20%.
(1)若建立函數![]() 模型制定獎勵方案,試用數學語言表述該公司對獎勵函數
模型制定獎勵方案,試用數學語言表述該公司對獎勵函數![]() 模型的基本要求,并分析函數
模型的基本要求,并分析函數![]() 是否符合公司要求的獎勵函數模型,并說明原因;
是否符合公司要求的獎勵函數模型,并說明原因;
(2)若該公司采用模型函數![]() 作為獎勵函數模型,試確定最小的正整數
作為獎勵函數模型,試確定最小的正整數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某商場2018年洗衣機、電視機和電冰箱三種電器各季度銷量的百分比堆積圖(例如:第3季度內,洗衣機銷量約占![]() ,電視機銷量約占
,電視機銷量約占![]() ,電冰箱銷量約占
,電冰箱銷量約占![]() ).根據該圖,以下結論中一定正確的是( )
).根據該圖,以下結論中一定正確的是( )
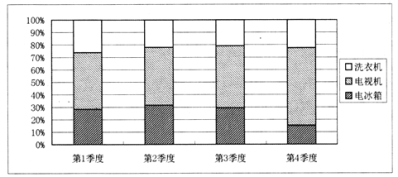
A. 電視機銷量最大的是第4季度
B. 電冰箱銷量最小的是第4季度
C. 電視機的全年銷量最大
D. 電冰箱的全年銷量最大
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】每年六、七月份,我國長江中下游地區進入持續25天左右的梅雨季節,如圖是江南某地區![]() 年10年間梅雨季節的降雨量
年10年間梅雨季節的降雨量![]() 單位:
單位:![]() 的頻率分布直方圖,試用樣本頻率估計總體概率,解答下列問題:
的頻率分布直方圖,試用樣本頻率估計總體概率,解答下列問題:

![]() 假設每年的梅雨季節天氣相互獨立,求該地區未來三年里至少有兩年梅雨季節的降雨量超過350mm的概率.
假設每年的梅雨季節天氣相互獨立,求該地區未來三年里至少有兩年梅雨季節的降雨量超過350mm的概率.
![]() 老李在該地區承包了20畝土地種植楊梅,他過去種植的甲品種楊梅,平均每年的總利潤為28萬元
老李在該地區承包了20畝土地種植楊梅,他過去種植的甲品種楊梅,平均每年的總利潤為28萬元![]() 而乙品種楊梅的畝產量
而乙品種楊梅的畝產量![]() 畝
畝![]() 與降雨量之間的關系如下面統計表所示,又知乙品種楊梅的單位利潤為
與降雨量之間的關系如下面統計表所示,又知乙品種楊梅的單位利潤為![]() 元
元![]() ,請你幫助老李分析,他來年應該種植哪個品種的楊梅可以使總利潤
,請你幫助老李分析,他來年應該種植哪個品種的楊梅可以使總利潤![]() 萬元
萬元![]() 的期望更大?并說明理由.
的期望更大?并說明理由.
降雨量 |
|
|
|
|
畝產量 | 500 | 700 | 600 | 400 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com