
如圖,在四棱錐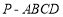 中,底面
中,底面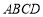 是矩形,側棱PD⊥底面
是矩形,側棱PD⊥底面 ,
,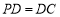 ,
,
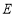 是
是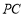 的中點,作
的中點,作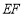 ⊥
⊥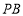 交
交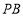 于點
于點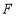 .
.

(1)證明: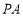 ∥平面
∥平面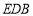 ;
;
(2)證明: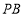 ⊥平面
⊥平面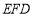 .
.
(1)詳見解析(2)詳見解析
【解析】
試題分析:(1)證明線面平行,往往利用其判定定理進行證明,即先證PA平行于平面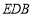 某一條直線,這可根據三角形中位線性質得到:連結
某一條直線,這可根據三角形中位線性質得到:連結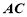 交
交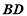 與
與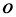 ,連結
,連結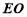 ,則點
,則點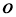 是
是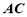 的中點. 又∵
的中點. 又∵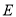 是
是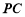 的中點,∴
的中點,∴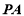 ∥
∥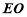 .而
.而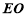
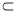 平面
平面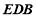 ,
,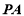
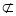 平面
平面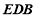 ,∴
,∴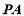 ∥平面
∥平面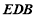
(2)證明線面垂直,往往利用其判定定理進行證明,即先證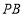 垂直平面
垂直平面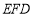 內兩條相交直線:已知
內兩條相交直線:已知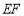 ⊥
⊥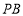 ,只需證
,只需證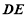 ⊥
⊥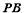 .由于
.由于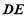 ⊥
⊥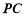 ,因此只需證
,因此只需證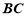 ⊥
⊥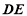 ,又由于
,又由于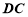 ⊥
⊥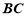 ,只需證
,只需證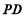 ⊥
⊥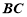 ,這可由
,這可由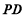 ⊥底面
⊥底面 得到.
得到.
試題解析:證明:(1)連結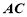 交
交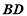 與
與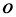 ,連結
,連結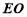 .
.
∵底面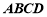 是矩形,
是矩形,
∴點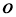 是
是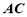 的中點.
的中點.
又∵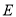 是
是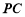 的中點
的中點
∴在△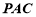 中,
中,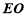 為中位線
為中位線
∴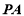 ∥
∥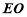 .
.
而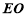
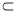 平面
平面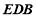 ,
,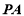
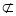 平面
平面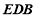 ,
,
∴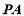 ∥平面
∥平面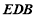 . 7分
. 7分
(2)由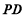 ⊥底面
⊥底面 ,得
,得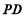 ⊥
⊥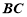 .
.
∵底面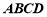 是正方形,
是正方形,
∴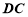 ⊥
⊥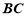 ,
,
∴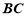 ⊥平面
⊥平面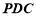 . 而
. 而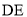
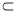 平面
平面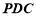 ,
,
∴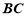 ⊥
⊥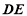 .①
.①
∵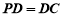 ,
,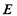 是
是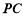 的中點,
的中點,
∴△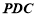 是等腰三角形,
是等腰三角形, 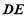 ⊥
⊥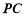 .②
.②
由①和②得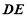 ⊥平面
⊥平面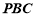 .
.
而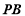
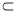 平面
平面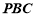 ,∴
,∴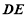 ⊥
⊥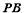 .
.
又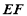 ⊥
⊥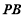 且
且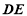
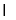
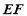 =
=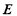 ,
,
∴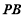 ⊥平面
⊥平面 . 14分
. 14分
考點:線面平行與垂直的判定定理


 小學課時特訓系列答案
小學課時特訓系列答案科目:高中數學 來源:2014-2015學年廣東省揭陽市高一上學期期中考試數學試卷(解析版) 題型:解答題
(本小題滿分14分)已知:定義在R上的函數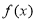 ,對于任意實數a, b都滿足
,對于任意實數a, b都滿足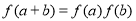 ,且
,且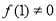 ,當
,當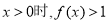 .
.
(Ⅰ)求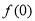 的值;
的值;
(Ⅱ)證明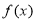 在
在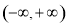 上是增函數;
上是增函數;
(Ⅲ)求不等式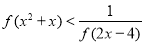 的解集.
的解集.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年江蘇省等五校高三12月第一次聯考文科數學試卷(解析版) 題型:解答題
函數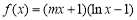 .
.
(1)若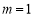 ,求曲線
,求曲線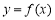 在
在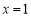 的切線方程;
的切線方程;
(2)若函數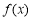 在
在 上是增函數,求實數
上是增函數,求實數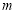 的取值范圍;
的取值范圍;
(3)設點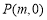 ,
,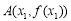 ,
,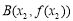 滿足
滿足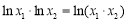
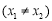 ,判斷是否存在實數
,判斷是否存在實數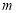 ,使得
,使得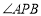 為直角?說明理由.
為直角?說明理由.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年江蘇省等五校高三12月第一次聯考理科數學試卷(解析版) 題型:解答題
選修4—1:幾何證明選講
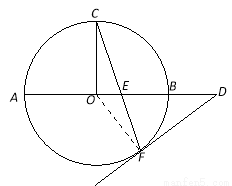
如圖,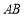 是⊙
是⊙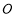 的直徑,
的直徑,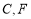 是⊙
是⊙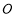 上的兩點,
上的兩點,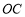 ⊥
⊥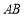 ,過點
,過點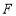 作⊙
作⊙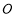 的切線FD交
的切線FD交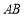 的延長線于點
的延長線于點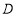 .連結
.連結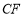 交
交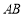 于點
于點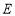 .
.
求證: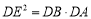 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com