日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
7．若x∈（-∞，2），則$\frac{{5-4x+{x^2}}}{2-x}$的最小值為2．

分析 y=$\frac{{5-4x+{x^2}}}{2-x}$=$2-x+\frac{1}{2-x}$，再利用均值不等式即可．

解答 解：y=$\frac{{5-4x+{x^2}}}{2-x}$=$\frac{（2-x）^{2}+1}{2-x}=2-x+\frac{1}{2-x}≥2$，（x＜2）
當且僅當x=1時取等號，則$\frac{{5-4x+{x^2}}}{2-x}$的最小值為2．
故答案為：2

點評 本題考查了構造均值不等式，求函數最值，屬于基礎題．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：填空題

17．若實數x0滿足f（x0）=x0，稱x0為函數f（x）的不動點．有下面三個命題：
（1）若f（x）是二次函數，且沒有不動點，則函數f（f（x））也沒有不動點；
（2）若f（x）是二次函數，則函數f（f（x））可能有4個不動點；
（3）若f（x）的不動點的個數是2，則f（f（x））的不動點的個數不可能是3．
它們中所有真命題的序號是（1）（2）．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

18．已知函數f（x）=ax2+2ax+4（-3＜a＜0），其圖象上兩點的橫坐標為x1、x&2滿足x1＜x2，且x1+x2=1+a，則由（　　）
A．f（x1）＜f（x2）B．f（x1）=f（x2）
C．f（x1）＞f（x2）D．f（x1）、f（x&2）的大小不確定

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

15．判斷函數f（x）=$\frac{{\sqrt{{x^2}+1}+x-1}}{{\sqrt{{x^2}+1}+x+1}}$的奇偶性（　　）
A．奇函數B．偶函數
C．既是奇函數又是偶函數D．非奇非偶函數

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

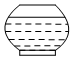2．一個高為H，容積為V的魚缸的軸截面如圖所示，向魚缸里注水，若魚缸里的水面高度為h時，魚缸里的水的體積為V'，則函數V'=f（h）的大致圖象可能是（　　）
A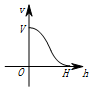．B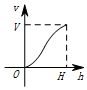．C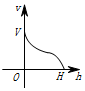．D．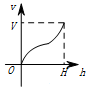

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

12．已知數列{an}滿足${a_1}=\frac{1}{3}$，${a_{n+1}}=\frac{a_n}{{2{a_n}+1}}，n∈{N^*}$
（1）求a2，a3，a4；
（2）是否存在正整數p，q使得對任意的n∈N*都有${a_n}=\frac{1}{pn+q}$，并用數學歸納法證明你的結論．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

19．定義在R上的函數f（x），滿足f（x+y）=f（x）+f（y）（x，y∈R），且f（1）=2，那么下面四個式子：
①f（1）+2f（1）+…+nf（1）；
②$f[\frac{n（n+1）}{2}]$；
③n（n+1）；
④n（n+1）f（1）
其中與f（1）+f（2）+…+f（n）（n∈N*）相等的是（　　）
A．①③B．①②C．①②③④D．①②③

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

16．求下列函數的導數
（1）y=x+ln（1+x）
（2）y=$\frac{sinx}{x-2}$．

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

17．（$\frac{4}{x}$）′=-$\frac{4}{{x}^{2}}$．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： av中文字幕在线播放 | 国产区在线观看 | 国产成人精品一区二区三区四区 | 亚洲一区视频 | 亚洲一区二区三区免费在线观看 | 玖玖国产精品视频 | 久一精品| 精品国产91乱码一区二区三区 | 一级免费视频 | 五月天电影网 | 午夜免费小视频 | 国产精品98| 欧美久久一级特黄毛片 | 伊人久操 | 成人免费在线 | 银杏成人影院在线观看 | 久久一二三区 | 中文字幕高清视频 | 久久青青操 | 日韩欧美国产成人一区二区 | 亚洲成人另类 | 欧美一级视频在线观看 | 亚洲精品一 | 99成人精品 | 欧美一级在线视频 | 国产日韩欧美 | 在线一区 | 日韩免费在线视频 | 久久靠逼 | 国产亚洲精品久久久久动 | 中文字幕日韩欧美一区二区三区 | 亚洲国产视频一区 | 欧美一区永久视频免费观看 | 亚洲一区二区av | 日日做夜夜操 | 国产精品久久久久久久免费大片 | 99热精品在线 | 99热国产在线观看 | 999久久国产 | 欧美精品在线一区二区三区 | 青青草久草 |