
【題目】某地政府為了對房地產(chǎn)市場進行調(diào)控決策,統(tǒng)計部門對外來人口和當(dāng)?shù)厝丝谶M行了買房的心理預(yù)期調(diào)研,用簡單隨機抽樣的方法抽取了110人進行統(tǒng)計,得到如下列聯(lián)表(不全):
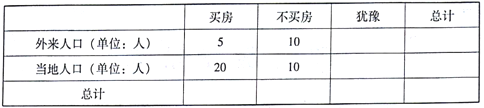
已知樣本中外來人口數(shù)與當(dāng)?shù)厝丝跀?shù)之比為3:8.
(1)補全上述列聯(lián)表;
(2)從參與調(diào)研的外來人口中用分層抽樣方法抽取6人,進一步統(tǒng)計外來人口的某項收入指標(biāo),若一個買房人的指標(biāo)記為3,一個猶豫人的指標(biāo)記為2,一個不買房人的指標(biāo)記為1,現(xiàn)在從這6人中再隨機選取3人,用![]() 表示這3人指標(biāo)之和,求
表示這3人指標(biāo)之和,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
【答案】(1)見解析(2)![]()
【解析】試題分析:(1)根據(jù)比例關(guān)系先確定外來人口數(shù)和當(dāng)?shù)厝丝跀?shù),求出猶豫人數(shù),填入表格即可,(2)先確定隨機變量的取法: ![]() ,再利用組合數(shù)分別求對應(yīng)概率,列表可得分布列,最后根據(jù)數(shù)學(xué)期望公式求數(shù)學(xué)期望
,再利用組合數(shù)分別求對應(yīng)概率,列表可得分布列,最后根據(jù)數(shù)學(xué)期望公式求數(shù)學(xué)期望
試題解析:解:(Ⅰ)設(shè)外來人口中和當(dāng)?shù)厝丝谥械莫q豫人數(shù)分別為![]() 人,
人, ![]() 人,則
人,則
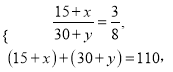 解得
解得![]()
買房 | 不買房 | 猶豫 | 總計 | |
外來人口(單位:人) | 5 | 10 | 15 | 30 |
當(dāng)?shù)厝丝冢▎挝唬喝耍?/span> | 20 | 10 | 50 | 80 |
總計 | 25 | 20 | 65 | 110 |
(Ⅱ)從參與調(diào)研的外來人口中用分層抽樣方法抽取的![]() 人中,買房1人,不買房2人,猶豫3人,所以
人中,買房1人,不買房2人,猶豫3人,所以![]() 的所有可能取值為
的所有可能取值為![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
所以![]() 的分布列為
的分布列為
X | 7 | 6 | 5 | 4 |
P |
|
|
|
|
所以![]() 的數(shù)學(xué)期望是
的數(shù)學(xué)期望是![]() .
.


 口算能手系列答案
口算能手系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 為坐標(biāo)原點,直線
為坐標(biāo)原點,直線![]() 的方程為
的方程為![]() ,點
,點![]() 是拋物線
是拋物線![]() 上到直線
上到直線![]() 距離最小的點,點
距離最小的點,點![]() 是拋物線上異于點
是拋物線上異于點![]() 的點,直線
的點,直線![]() 與直線
與直線![]() 交于點
交于點![]() ,過點
,過點![]() 與
與![]() 軸平行的直線與拋物線
軸平行的直線與拋物線![]() 交于點
交于點![]() .
.
(1)求點![]() 的坐標(biāo);
的坐標(biāo);
(2)求證:直線![]() 恒過定點
恒過定點![]() ;
;
(3)在(2)的條件下過![]() 向
向![]() 軸做垂線,垂足為
軸做垂線,垂足為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在三棱錐A﹣BCD中,AB⊥平面BCD,BC⊥CD,且AB=3,BD=4,則三棱錐A﹣BCD外接球的半徑為( )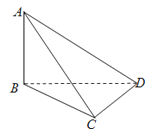
A.2
B.3
C.4
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是正方形,側(cè)棱PD⊥底面ABCD,PD=DC=2,E是PC的中點,作EF⊥PB交PB于點F.
(1)證明:PA∥平面EDB;
(2)證明:PB⊥平面EFD.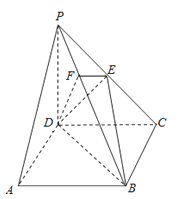
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,坐標(biāo)平面上一點P滿足:
,坐標(biāo)平面上一點P滿足: ![]() 的周長為6,記點P的軌跡為
的周長為6,記點P的軌跡為![]() .拋物線
.拋物線![]() 以
以![]() 為焦點,頂點為坐標(biāo)原點O.
為焦點,頂點為坐標(biāo)原點O.
(Ⅰ)求![]() ,
, ![]() 的方程;
的方程;
(Ⅱ)若過![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,問在
兩點,問在![]() 上且在直線
上且在直線![]() 外是否存在一點
外是否存在一點![]() ,使直線
,使直線![]() 的斜率依次成等差數(shù)列,若存在,請求出點
的斜率依次成等差數(shù)列,若存在,請求出點![]() 的坐標(biāo),若不存在,請說明理由.
的坐標(biāo),若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知三棱柱ABC﹣A′B′C′,側(cè)棱與底面垂直,且所有的棱長均為2,E為AA′的中點,F(xiàn)為AB的中點. (Ⅰ)求多面體ABCB′C′E的體積;
(Ⅱ)求異面直線C'E與CF所成角的余弦值.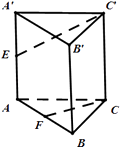
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系中,曲線![]() 的普通方程為
的普通方程為![]() ,曲線
,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() 為參數(shù)),以坐標(biāo)原點為極點,
為參數(shù)),以坐標(biāo)原點為極點, ![]() 軸正半軸為極軸建立極坐標(biāo)系.
軸正半軸為極軸建立極坐標(biāo)系.
(1)求曲線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)求曲線![]() 與
與![]() 焦點的極坐標(biāo)
焦點的極坐標(biāo)![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,設(shè)F1、F2分別為橢圓的左、右焦點,橢圓上任意一個動點M到左焦點F1的距離的最大值 為
,設(shè)F1、F2分別為橢圓的左、右焦點,橢圓上任意一個動點M到左焦點F1的距離的最大值 為 ![]() +1 (Ⅰ)求橢圓C的方程;
+1 (Ⅰ)求橢圓C的方程;
(Ⅱ)設(shè)直線L的斜率為k,且過左焦點F1 , 與橢圓C相交于P、Q兩點,若△PQF2的面積為 ![]() ,試求k的值及直線L的方程.
,試求k的值及直線L的方程.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com