
【題目】已知![]() ,坐標平面上一點P滿足:
,坐標平面上一點P滿足: ![]() 的周長為6,記點P的軌跡為
的周長為6,記點P的軌跡為![]() .拋物線
.拋物線![]() 以
以![]() 為焦點,頂點為坐標原點O.
為焦點,頂點為坐標原點O.
(Ⅰ)求![]() ,
, ![]() 的方程;
的方程;
(Ⅱ)若過![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,問在
兩點,問在![]() 上且在直線
上且在直線![]() 外是否存在一點
外是否存在一點![]() ,使直線
,使直線![]() 的斜率依次成等差數列,若存在,請求出點
的斜率依次成等差數列,若存在,請求出點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分別是AP、AD的中點,求證:
(1)直線EF∥平面PCD;
(2)平面BEF⊥平面PAD.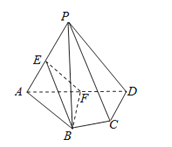
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() 與
與![]() 的等差中項為
的等差中項為![]() (
(![]() ).
).
(1)求數列![]() 的通項公式;
的通項公式;
(2)是否存在正整數![]() ,是不等式
,是不等式![]() (
(![]() )恒成立,若存在,求出
)恒成立,若存在,求出![]() 的最大值;若不存在,請說明理由.
的最大值;若不存在,請說明理由.
(3)設
![]() ,若集合
,若集合![]() 恰有
恰有![]() 個元素,求實數
個元素,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形![]() 是正四棱柱
是正四棱柱![]() 的一個截面,此截面與棱
的一個截面,此截面與棱![]() 交于點
交于點![]() ,
, ![]() ,其中
,其中![]() 分別為棱
分別為棱![]() 上一點.
上一點.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)![]() 為線段
為線段![]() 上一點,若四面體
上一點,若四面體![]() 與四棱錐
與四棱錐![]() 的體積相等,求
的體積相等,求![]() 的長.
的長.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2+2x﹣4y+3=0.
(1)若圓C的切線在x軸和y軸上的截距相等,求此切線的方程;
(2)從圓C外一點P(x1 , y1)向該圓引一條切線,切點為M,O為坐標原點,且有|PM|=|PO|,求使得|PM|取得最小值的點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地政府為了對房地產市場進行調控決策,統計部門對外來人口和當地人口進行了買房的心理預期調研,用簡單隨機抽樣的方法抽取了110人進行統計,得到如下列聯表(不全):
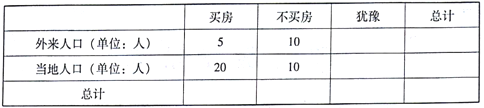
已知樣本中外來人口數與當地人口數之比為3:8.
(1)補全上述列聯表;
(2)從參與調研的外來人口中用分層抽樣方法抽取6人,進一步統計外來人口的某項收入指標,若一個買房人的指標記為3,一個猶豫人的指標記為2,一個不買房人的指標記為1,現在從這6人中再隨機選取3人,用![]() 表示這3人指標之和,求
表示這3人指標之和,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,四棱錐P﹣ABCD的底面ABCD是邊長為1的菱形,∠BCD=60°,E是CD的中點,PA⊥底面ABCD,PA=![]() .
.
(Ⅰ)證明:平面PBE⊥平面PAB;
(Ⅱ)求二面角A﹣BE﹣P的大小.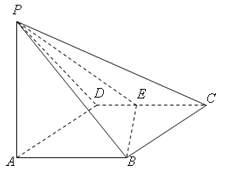
查看答案和解析>>
科目:高中數學 來源: 題型:
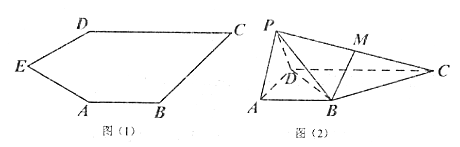
【題目】如圖(1)五邊形![]() 中,
中, ![]()
![]() ,將
,將![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱錐
的位置,得到四棱錐![]() ,如圖(2),點
,如圖(2),點![]() 為線段
為線段![]() 的中點,且
的中點,且![]() 平面
平面![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若四棱柱![]() 的體積為
的體積為![]() ,求四面體
,求四面體![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com