
【題目】如圖,在四棱錐P﹣ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分別是AP、AD的中點,求證:
(1)直線EF∥平面PCD;
(2)平面BEF⊥平面PAD.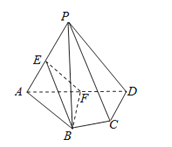
【答案】證明:(1)在△PAD中,因為E,F分別為AP,AD的中點,所以EF∥PD.
又因為EF不在平面PCD中,PD平面PCD
所以直線EF∥平面PCD.
(2)連接BD.因為AB=AD,∠BAD=60°.
所以△ABD為正三角形.因為F是AD的中點,所以BF⊥AD.
因為平面PAD⊥平面ABCD,BF平面ABCD,
平面PAD∩平面ABCD=AD,所以BF⊥平面PAD.
又因為BF平面EBF,所以平面BEF⊥平面PAD.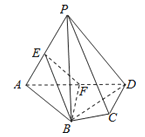
【解析】(1)要證直線EF∥平面PCD,只需證明EF∥PD,EF不在平面PCD中,PD平面PCD即可.
(2)連接BD,證明BF⊥AD.說明平面PAD∩平面ABCD=AD,推出BF⊥平面PAD;然后證明平面BEF⊥平面PAD.


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:高中數學 來源: 題型:
【題目】第96屆(春季)全國糖酒商品交易會于2017年3月23日至25日在四川舉辦.交易會開始前,展館附近一家川菜特色餐廳為了研究參會人數與餐廳所需原材料數量的關系,查閱了最近5次交易會的參會人數![]() (萬人)與餐廳所用原材料數量
(萬人)與餐廳所用原材料數量![]() (袋),得到如下數據:
(袋),得到如下數據:

(Ⅰ)請根據所給五組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(Ⅱ)已知購買原材料的費用![]() (元)與數量
(元)與數量![]() (袋)的關系為
(袋)的關系為![]() 投入使用的每袋原材料相應的銷售收入為600元,多余的原材料只能無償返還.若餐廳原材料現恰好用完,據悉本次交易會大約有14萬人參加,根據(Ⅰ)中求出的線性回歸方程,預測餐廳應購買多少袋原材料,才能獲得最大利潤,最大利潤是多少?(注:利潤
投入使用的每袋原材料相應的銷售收入為600元,多余的原材料只能無償返還.若餐廳原材料現恰好用完,據悉本次交易會大約有14萬人參加,根據(Ⅰ)中求出的線性回歸方程,預測餐廳應購買多少袋原材料,才能獲得最大利潤,最大利潤是多少?(注:利潤![]() 銷售收入
銷售收入![]() 原材料費用).
原材料費用).
(參考公式: 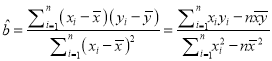 ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,直線
為坐標原點,直線![]() 的方程為
的方程為![]() ,點
,點![]() 是拋物線
是拋物線![]() 上到直線
上到直線![]() 距離最小的點,點
距離最小的點,點![]() 是拋物線上異于點
是拋物線上異于點![]() 的點,直線
的點,直線![]() 與直線
與直線![]() 交于點
交于點![]() ,過點
,過點![]() 與
與![]() 軸平行的直線與拋物線
軸平行的直線與拋物線![]() 交于點
交于點![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)求證:直線![]() 恒過定點
恒過定點![]() ;
;
(3)在(2)的條件下過![]() 向
向![]() 軸做垂線,垂足為
軸做垂線,垂足為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,坐標平面上一點P滿足:
,坐標平面上一點P滿足: ![]() 的周長為6,記點P的軌跡為
的周長為6,記點P的軌跡為![]() .拋物線
.拋物線![]() 以
以![]() 為焦點,頂點為坐標原點O.
為焦點,頂點為坐標原點O.
(Ⅰ)求![]() ,
, ![]() 的方程;
的方程;
(Ⅱ)若過![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,問在
兩點,問在![]() 上且在直線
上且在直線![]() 外是否存在一點
外是否存在一點![]() ,使直線
,使直線![]() 的斜率依次成等差數列,若存在,請求出點
的斜率依次成等差數列,若存在,請求出點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com