
【題目】如圖,平面![]() 平面
平面![]() ,其中
,其中![]() 為矩形,
為矩形,![]() 為梯形,
為梯形,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)若二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() ,求
,求![]() 的長.
的長.

【答案】(Ⅰ)見解析; (Ⅱ)![]() .
.
【解析】
(Ⅰ)由條件易得![]() 和
和![]() ,從而可證得
,從而可證得![]() 平面
平面![]() ;
;
(Ⅱ)設AB=x.以F為原點,AF,FE所在的直線分別為x軸,y軸建立空間直角坐標系,平面ABF的法向量可取![]() =(0,1,0),通過求解平面BFD的法向量
=(0,1,0),通過求解平面BFD的法向量![]() ,進而利用法向量求二面角的余弦值列方程求解即可.
,進而利用法向量求二面角的余弦值列方程求解即可.
(Ⅰ)![]() 平面
平面![]() 平面
平面![]() ,且
,且![]() 為矩形,
為矩形,
![]()
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]()
![]() ,又
,又![]() 且
且![]()
![]() 平面
平面![]() .
.
(Ⅱ)設AB=x.以F為原點,AF,FE所在的直線分別為x軸,y軸建立空間直角坐標系![]() .
.
則F(0,0,0),A(-2,0,0),E(0,![]() ,0),D(-1,
,0),D(-1,![]() ,0),B(-2,0,x),
,0),B(-2,0,x),
所以![]() =(1,-
=(1,-![]() ,0),
,0),![]() =(2,0,-x).
=(2,0,-x).
因為EF⊥平面ABF,所以平面ABF的法向量可取![]() =(0,1,0).
=(0,1,0).
設![]() =(x1,y1,z1)為平面BFD的法向量,
=(x1,y1,z1)為平面BFD的法向量,
則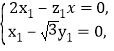 所以,可取
所以,可取![]() =(
=(![]() ,1,
,1,![]() ).
).
因為cos<![]() ,
,![]() >=
>=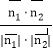 =
=![]() ,得x=
,得x=![]() ,所以AB=
,所以AB=![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數y=a-bcos![]() (b>0)的最大值為
(b>0)的最大值為![]() ,最小值為-
,最小值為-![]() .
.
(1)求a,b的值;
(2)求函數g(x)=-4asin![]() 的最小值并求出對應x的集合.
的最小值并求出對應x的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下是某地搜集到的新房屋的銷售價格![]() 和房屋的面積
和房屋的面積![]() 的數據:
的數據:
房屋面積( | 115 | 110 | 80 | 135 | 105 |
銷售價格(萬元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)畫出數據對應的散點圖;
(2)求線性回歸方程,并在散點圖中加上回歸直線;
(3)據(2)的結果估計當房屋面積為150![]() 時的銷售價格.附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
時的銷售價格.附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
 ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確的是( )
A.經過任意三點有且只有一個平面.
B.過點![]() 有且僅有一條直線與異面直線
有且僅有一條直線與異面直線![]() 垂直.
垂直.
C.一條直線與一個平面平行,它就和這個平面內的任意一條直線平行.
D.面![]() 與平面
與平面![]() 相交,則公共點個數為有限個.
相交,則公共點個數為有限個.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為推行“新課堂”教學法,某化學老師分別用傳統教學和“新課堂”兩種不同的教學方式,在甲、乙兩個平行班級進行教學實驗.為了比較教學效果,期中考試后,分別從兩個班級中各隨機抽取20名學生的成績進行統計,結果如下表:記成績不低于70分者為“成績優良”.
分數 |
|
|
|
|
|
甲班頻數 | 5 | 6 | 4 | 4 | 1 |
乙班頻數 | 1 | 3 | 6 | 5 | 5 |
(1)由以上統計數據填寫下面![]() 列聯表,并判斷能否在犯錯概率不超過0.025的前提下認為“成績優良與教學方式有關”?
列聯表,并判斷能否在犯錯概率不超過0.025的前提下認為“成績優良與教學方式有關”?
甲班 | 乙班 | 總計 | |
成績優良 | |||
成績不優良 | |||
總計 |
附: ,其中
,其中![]() .
.
臨界值表
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
(2)現從上述40人中,學校按成績是否優良采用分層抽樣的方法抽取8人進行考核.在這8人中,記成績不優良的乙班人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海洋藍洞是地球罕見的自然地理現象,被喻為“地球留給人類保留宇宙秘密的最后遺產”,我國擁有世界上最深的海洋藍洞,若要測量如圖所示的藍洞的口徑![]() ,
,![]() 兩點間的距離,現在珊瑚群島上取兩點
兩點間的距離,現在珊瑚群島上取兩點![]() ,
,![]() ,測得
,測得![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() 兩點的距離為___.
兩點的距離為___.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,![]() 是海面上一條南北方向的海防警戒線,在
是海面上一條南北方向的海防警戒線,在 ![]() 上點
上點 ![]() 處有一個水聲監測點,另兩個監測點
處有一個水聲監測點,另兩個監測點 ![]() 分別在
分別在 ![]() 的正東方向
的正東方向 ![]() 處和
處和 ![]() 處.某時刻,監測點
處.某時刻,監測點 ![]() 收到發自目標
收到發自目標 ![]() 的一個聲波,
的一個聲波,![]() 后監測點
后監測點 ![]() 后監測點
后監測點 ![]() 相繼收到這一信號,在當時的氣象條件下,聲波在水中的傳播速度是
相繼收到這一信號,在當時的氣象條件下,聲波在水中的傳播速度是 ![]() .
.

(1)設 ![]() 到
到 ![]() 的距離為
的距離為 ![]() ,用
,用 ![]() 分別表示
分別表示 ![]() 到
到 ![]() 的距離,并求
的距離,并求 ![]() 的值;
的值;
(2)求目標 ![]() 的海防警戒線
的海防警戒線 ![]() 的距離(精確到
的距離(精確到 ![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】山東省于2015年設立了水下考古研究中心,以此推動全省的水下考古、水下文化遺產保護等工作;水下考古研究中心工作站,分別設在位于劉公島的中國甲午戰爭博物院和威海市博物館。為對劉公島周邊海域水底情況進行詳細了解,然后再選擇合適的時機下水探摸、打撈,省水下考古中心在一次水下考古活動中,某一潛水員需潛水![]() 米到水底進行考古作業,其用氧量包含以下三個方面:
米到水底進行考古作業,其用氧量包含以下三個方面:
①下潛平均速度為![]() 米/分鐘,每分鐘的用氧量為
米/分鐘,每分鐘的用氧量為![]() 升;
升;
②水底作業時間范圍是最少10分鐘最多20分鐘,每分鐘用氧量為0.4升;
③返回水面時,平均速度為![]() 米/分鐘,每分鐘用氧量為0.32升.
米/分鐘,每分鐘用氧量為0.32升.
潛水員在此次考古活動中的總用氧量為![]() 升.
升.
(Ⅰ)如果水底作業時間是![]() 分鐘,將
分鐘,將![]() 表示為
表示為![]() 的函數;
的函數;
(Ⅱ)若![]() ,水底作業時間為20分鐘,求總用氧量
,水底作業時間為20分鐘,求總用氧量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com