
【題目】設點P是直線![]() 上一點,過點P分別作拋物線
上一點,過點P分別作拋物線![]() 的兩條切線
的兩條切線![]() ,其中A、B為切點.
,其中A、B為切點.
(1)若點A的坐標為![]() ,求點P的橫坐標;
,求點P的橫坐標;
(2)當![]() 的面積為
的面積為![]() 時,求
時,求![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由導數的幾何意義,可先求直線切線![]() 的斜率
的斜率![]() ,由點斜式寫出直線
,由點斜式寫出直線![]() 方程,再由點
方程,再由點![]() 縱坐標為-2代入直線方程即可求解;
縱坐標為-2代入直線方程即可求解;
(2)設![]() ,分別表示出直線
,分別表示出直線![]() 的方程為
的方程為![]() ,同理得
,同理得![]() ,由兩直線均過
,由兩直線均過![]() 得
得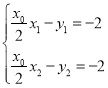 ,可推出直線方程為
,可推出直線方程為![]() ,聯立拋物線方程
,聯立拋物線方程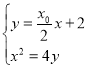 解出關于
解出關于![]() 的一元二次方程,結合弦長公式和點到直線距離公式表示出三角形面積公式為
的一元二次方程,結合弦長公式和點到直線距離公式表示出三角形面積公式為![]() ,即可求解
,即可求解![]() ,進而求解弦長
,進而求解弦長![]() ;還可設
;還可設![]() ,將
,將![]() 兩點縱坐標結合拋物線代換,表示出直線
兩點縱坐標結合拋物線代換,表示出直線![]() 的方程為
的方程為![]() ,同理直線
,同理直線![]() 的方程為
的方程為![]() ,聯立解得
,聯立解得![]() ,故
,故![]() ,設直線
,設直線![]() 的方程為
的方程為![]() ,聯立
,聯立 ,推出參數
,推出參數![]() ,后續求解步驟同前一種解法
,后續求解步驟同前一種解法
(1)由![]() ,所以
,所以![]() ,
,
因為![]() ,
,
由導數的幾何意義知,切線![]() 的斜率
的斜率![]() ,
,
所以切線![]() 的方程為
的方程為![]() ,即
,即![]() ,
,
又因為點P為直線![]() 與直線
與直線![]() 的公共點,
的公共點,
聯立![]() 與
與![]() ,可得P點橫坐標為
,可得P點橫坐標為![]() .
.
(2)法一:不妨設![]() ,
,
由(1)可知![]() ,即直線
,即直線![]() 的方程為
的方程為![]() ,
,
即![]() ,同理可得
,同理可得![]()
因為切線![]() 均過點
均過點![]() ,所以
,所以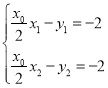 ,
,
所以![]() 為方程
為方程![]() 的兩組解,
的兩組解,
所以直線![]() 的方程為
的方程為![]() ,即
,即![]()
聯立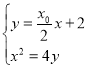 ,可得
,可得![]() ,顯然
,顯然![]() ,
,
由韋達定理得,![]() ,
,
所以 ,
,
又因為點P到直線![]() 的距離
的距離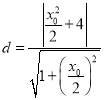 ,
,
所以 ,
,
解得![]() ,所以
,所以![]() .
.
法二:不妨設![]() ,由(1)可知直線
,由(1)可知直線![]() 的方程為
的方程為![]() ,
,
同理,直線![]() 的方程為
的方程為![]() ,
,
聯立解得![]() ,
,
又點P在直線![]() ,所以
,所以![]() ,
,
設直線![]() 的方程為
的方程為![]() ,聯立
,聯立 ,可得
,可得![]() ,
,
由韋達定理得![]() ,
,
可得![]() ,
,
所以![]() ,
,
又因為點P到直線![]() 的距離為
的距離為 ,
,
所以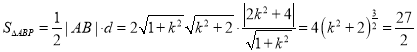 ,
,
解得![]() ,所以
,所以![]() .
.


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:高中數學 來源: 題型:
【題目】已知二面角α﹣l﹣β為60°,在其內部取點A,在半平面α,β內分別取點B,C.若點A到棱l的距離為1,則△ABC的周長的最小值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業引進現代化管理體制,生產效益明顯提高.2018年全年總收入與2017年全年總收入相比增長了一倍,實現翻番.同時該企業的各項運營成本也隨著收入的變化發生了相應變化.下圖給出了該企業這兩年不同運營成本占全年總收入的比例,下列說法正確的是( )
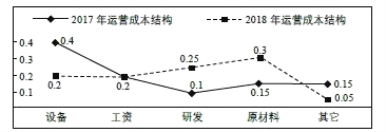
A.該企業2018年原材料費用是2017年工資金額與研發費用的和
B.該企業2018年研發費用是2017年工資金額、原材料費用、其它費用三項的和
C.該企業2018年其它費用是2017年工資金額的![]()
D.該企業2018年設備費用是2017年原材料的費用的兩倍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面多邊形![]() 中,四邊形
中,四邊形![]() 是邊長為2的正方形,四邊形
是邊長為2的正方形,四邊形![]() 為等腰梯形,
為等腰梯形,![]() 為
為![]() 的中點,
的中點,![]() ,現將梯形
,現將梯形![]() 沿
沿![]() 折疊,使平面
折疊,使平面![]() 平面
平面![]() .
.
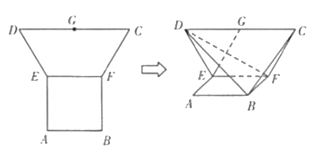
(1)求證:![]() 面
面![]() ;
;
(2)求![]() 與平面
與平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十九世紀末,法國學者貝特朗在研究幾何概型時提出了“貝特朗悖論”,即“在一個圓內任意選一條弦,這條弦的弦長長于這個圓的內接等邊三角形邊長的概率是多少?”貝特朗用“隨機半徑”、“隨機端點”、“隨機中點”三個合理的求解方法,但結果都不相同.該悖論的矛頭直擊概率概念本身,強烈地刺激了概率論基礎的嚴格化.已知“隨機端點”的方法如下:設A為圓O上一個定點,在圓周上隨機取一點B,連接AB,所得弦長AB大于圓O的內接等邊三角形邊長的概率.則由“隨機端點”求法所求得的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年是中國改革開放的第40周年,為了充分認識新形勢下改革開放的時代性,某地的民調機構隨機選取了該地的100名市民進行調查,將他們的年齡分成6段:![]() ,并繪制了如圖所示的頻率分布直方圖.
,并繪制了如圖所示的頻率分布直方圖.
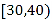
(1)現從年齡在![]() 內的人員中按分層抽樣的方法抽取8人,再從這8人中隨機抽取3人進行座談,用
內的人員中按分層抽樣的方法抽取8人,再從這8人中隨機抽取3人進行座談,用![]() 表示年齡在
表示年齡在![]() 內的人數,求
內的人數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)若用樣本的頻率代替概率,用隨機抽樣的方法從該地抽取20名市民進行調查,其中有![]() 名市民的年齡在
名市民的年齡在![]() 的概率為
的概率為![]() .當
.當![]() 最大時,求
最大時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在①![]() ;②
;②![]() ;③
;③![]() 這三個條件中任選一個,補充在下面問題中的橫線上,并解答相應的問題.
這三個條件中任選一個,補充在下面問題中的橫線上,并解答相應的問題.
在![]() 中,內角A,B,C的對邊分別為a,b,c,且滿足________________,
中,內角A,B,C的對邊分別為a,b,c,且滿足________________,![]()
![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com