
【題目】已知函數![]() ,有下列四個結論:
,有下列四個結論:
①![]() 為偶函數;②
為偶函數;②![]() 的值域為
的值域為![]() ;
;
③![]() 在
在![]() 上單調遞減;④
上單調遞減;④![]() 在
在![]() 上恰有8個零點,
上恰有8個零點,
其中所有正確結論的序號為( )
A.①③B.②④C.①②③D.①③④
【答案】A
【解析】
由偶函數的定義可判斷①正確,借助二倍角公式將函數化簡為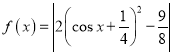 利用二次函數性質計算可得②錯誤,利用復合函數的單調性可判斷
利用二次函數性質計算可得②錯誤,利用復合函數的單調性可判斷![]() 在
在![]() 上單調遞減,且
上單調遞減,且![]() ,則
,則![]() 在
在![]() 上單調遞增,根據偶函數性質可得出③正確,利用函數與方程的思想解方程即可判斷④錯誤.
上單調遞增,根據偶函數性質可得出③正確,利用函數與方程的思想解方程即可判斷④錯誤.
由![]() ,故
,故![]() 為偶函數,①正確;
為偶函數,①正確;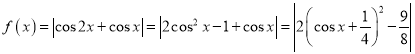 ,
,
記![]() ,則
,則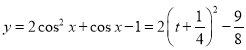 ,
,
當![]() 時,
時,![]() 取得最大值2,當
取得最大值2,當![]() 時,
時,![]() 取9得最小值
取9得最小值![]() ,
,
即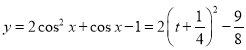 的值域為
的值域為![]() ,所以
,所以![]() 的值域為
的值域為![]() ,②錯誤;
,②錯誤;
![]() 在
在![]() 上的單調性與它在
上的單調性與它在![]() 上的單調性剛好相反,
上的單調性剛好相反,
當![]() 時,
時,![]() 單調遞增,且
單調遞增,且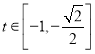 ,而
,而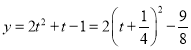 在
在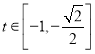 時單調遞減,
時單調遞減,
故![]() 在
在![]() 上單調遞減,又此時
上單調遞減,又此時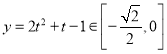 ,故函數
,故函數![]() 在
在![]() 上單調遞增,于是得
上單調遞增,于是得![]() 在
在![]() 單調遞減,③正確;
單調遞減,③正確;
令![]() ,得
,得![]() 或
或![]() ,而當
,而當![]() 時,
時,![]() 及
及![]() 恰有3個不等的實根
恰有3個不等的實根![]() ,
,![]() ,
,![]() ,
,
即![]() 在區間
在區間![]() 上恰有3個零點,結合奇偶性可知,即
上恰有3個零點,結合奇偶性可知,即![]() 在區間
在區間![]() 上恰有6個零點,④錯誤.
上恰有6個零點,④錯誤.
故正確的是①③.
故選:A.


 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+1|﹣|2x﹣2|的最大值為M,正實數a,b滿足a+b=M.
(1)求2a2+b2的最小值;
(2)求證:aabb≥ab.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖![]() ,在邊長為
,在邊長為![]() 的菱形
的菱形![]() 中,
中,![]() ,現沿對角線
,現沿對角線![]() 把
把![]() 翻折到
翻折到![]() 的位置得到四面體
的位置得到四面體![]() ,如圖
,如圖![]() 所示.已知
所示.已知![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是線段
是線段![]() 上的點,且
上的點,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過右焦點F的直線L與C相交于A、B兩點,當L的斜率為1時,坐標原點O到L的距離為
,過右焦點F的直線L與C相交于A、B兩點,當L的斜率為1時,坐標原點O到L的距離為![]() .
.
(1)求橢圓的標準方程;
(2)在C上是否存在點P,使得當L繞F轉到某一位置時,有![]() 成立?若存在,求出所有的P的坐標與L的方程;若不存在,說明理由.
成立?若存在,求出所有的P的坐標與L的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】今年情況特殊,小王在居家自我隔離時對周邊的水產養殖產業進行了研究.![]() 、
、![]() 兩個投資項目的利潤率分別為投資變量
兩個投資項目的利潤率分別為投資變量![]() 和
和![]() .根據市場分析,
.根據市場分析,![]() 和
和![]() 的分布列分別為:
的分布列分別為:
| 5% | 10% | ||
| 0.8 | 0.2 | ||
| 2% | 8% | 12% | |
| 0.2 | 0.5 | 0.3 | |
(1)若在![]() 兩個項目上各投資
兩個項目上各投資![]() 萬元,
萬元,![]() 和
和![]() 分別表示投資項目
分別表示投資項目![]() 和
和![]() 所獲得的利潤,求方差
所獲得的利潤,求方差![]() ,
,![]() ;
;
(2)若在![]() 兩個項目上共投資
兩個項目上共投資![]() 萬元,那么如何分配,能使投資
萬元,那么如何分配,能使投資![]() 項目所得利潤的方差與投資
項目所得利潤的方差與投資![]() 項目所得利潤的方差的和最小,最小值是多少?
項目所得利潤的方差的和最小,最小值是多少?
(注:![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com