
分析 (1)根據函數的單調性求出m的范圍,從而求出m的值;
(2)根據函數的奇偶性得到f(a+1)<f(4-3a),根據函數在R上遞增,得到a+1<4-3a,求出a的范圍即可.
解答 解 (1)∵函數在(0,+∞)上遞增,
∴9-3m>0,解得m<3,…(2分)
又m∈N*,
∴m=1,2.…(3分)
又函數圖象關于原點對稱,
∴3m-9為奇數,故m=2.…(5分)
∴f(x)=x3…(6分)
(2)∵f(a+1)+f(3a-4)<0,
∴f(a+1)<-f(3a-4)…(7分)
又f(x)為奇函數,
∴f(a+1)<f(4-3a)…(9分)
又函數在R上遞增,
∴a+1<4-3a…(11分)
∴$a<\frac{3}{4}$.…(12分)
點評 本題考查了冪函數的性質,考查函數的單調性、奇偶性問題,是一道中檔題.


科目:高中數學 來源: 題型:解答題
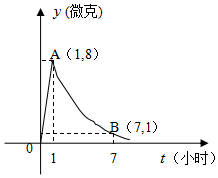 某醫藥研究所開發一種新藥,據監測,如果成人按規定的劑量服用,服用藥后每毫升中的含藥量y(微克)與服藥的時間t(小時)之間近似滿足如圖所示的曲線,其中OA是線段,曲線AB是函數y=kat(t≥1,a>0,且k,a是常數)的圖象.
某醫藥研究所開發一種新藥,據監測,如果成人按規定的劑量服用,服用藥后每毫升中的含藥量y(微克)與服藥的時間t(小時)之間近似滿足如圖所示的曲線,其中OA是線段,曲線AB是函數y=kat(t≥1,a>0,且k,a是常數)的圖象.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
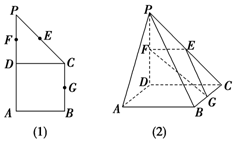 如圖(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分別為線段PC、PD、BC的中點,現將△PDC折起,使平面PDC⊥平面ABCD(圖(2)).
如圖(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分別為線段PC、PD、BC的中點,現將△PDC折起,使平面PDC⊥平面ABCD(圖(2)).查看答案和解析>>
科目:高中數學 來源: 題型:解答題
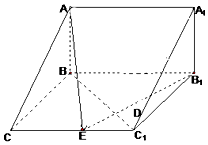 如圖,在三棱柱ABC-A1B1C1中,已知AB⊥側面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1=$\sqrt{2}$,
如圖,在三棱柱ABC-A1B1C1中,已知AB⊥側面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1=$\sqrt{2}$,查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com