
分析 (1)求出函數的定義域,求出導函數,根據導函數討論參數a,得出函數的單調區間;
(2)構造函數令h(x)=ax-f(x),則$h(x)=2ax-ln({x+\frac{1}{a}})$.問題轉化為h(x)>0恒成立時a的取值范圍.對參數a進行分類討論,利用導函數得出函數的最值即可.
解答 解:(1)f(x)的定義域為$({-\frac{1}{a},+∞})$,且$f'(x)=\frac{1}{{x+\frac{1}{a}}}-a=-\frac{{{a^2}x}}{ax+1}$.
①當a<0時,∵$x>-\frac{1}{a}$,∴ax<-1,∴f'(x)>0,函數在$({-\frac{1}{a},+∞})$是增函數;
②當a>0時,ax+1>0,在區間$({-\frac{1}{a},0})$上,f'(x)>0;在區間(0,+∞)上,f'(x)<0.
所以f(x)在區間$({-\frac{1}{a},0})$上是增函數;在區間(0,+∞)上是減函數.
(2)令h(x)=ax-f(x),則$h(x)=2ax-ln({x+\frac{1}{a}})$.
問題轉化為h(x)>0恒成立時a的取值范圍.
當a<0時,取$x=e-\frac{1}{a}$,則h(x)=2ae-3<0,不合題意.
當a>0時,h(x)=ax-f(x),則$h(x)=2ax-ln({x+\frac{1}{a}})$.
由于$h'(x)=2a-\frac{1}{{x+\frac{1}{a}}}=\frac{{2a({x+\frac{1}{2a}})}}{{x+\frac{1}{a}}}$,
所以在區間$({-\frac{1}{a},-\frac{1}{2a}})$上,h'(x)<0;在區間$({-\frac{1}{2a},+∞})$上,h'(x)>0.
所以h(x)的最小值為$h({-\frac{1}{2a}})$,
所以只需$h({-\frac{1}{2a}})>0$,即$2a•({-\frac{1}{2a}})-ln({-\frac{1}{2a}+\frac{1}{a}})>0$,
所以$ln\frac{1}{2a}<-1$,
所以$a>\frac{e}{2}$.
點評 本題考查了導函數的綜合應用,難點是對參數的分類討論和構造函數,把恒成立問題轉換為最值問題.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{9}$ | B. | $\frac{5π}{18}$ | C. | $\frac{7π}{18}$ | D. | $\frac{11π}{18}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| x | 4 | 6 | 8 | 10 | 12 |
| y | 1 | 2 | 3 | 5 | 6 |
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
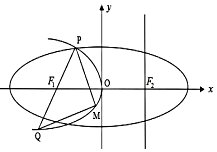 如圖,設拋物線C1:y2=-4mx(m>0)的準線l與x軸交于橢圓C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦點F2,F1為C2的左焦點.橢圓的離心率為e=$\frac{1}{2}$,拋物線C1與橢圓C2交于x軸上方一點P,連接PF1并延長其交C1于點Q,M為C1上一動點,且在P,Q之間移動.
如圖,設拋物線C1:y2=-4mx(m>0)的準線l與x軸交于橢圓C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦點F2,F1為C2的左焦點.橢圓的離心率為e=$\frac{1}{2}$,拋物線C1與橢圓C2交于x軸上方一點P,連接PF1并延長其交C1于點Q,M為C1上一動點,且在P,Q之間移動.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 學校 | A | B | C | D |
| 語文(x分) | 118 | 120 | 114 | 112 |
| 數學 (y分) | 116 | 123 | 114 | 119 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖所示,某幼兒園有一個游樂場ABCD,其中AB=50米,BC=40米,由于幼兒園招生規模增大,需將該游樂場擴大成矩形區域EFGH,要求A、B、C、D四個點分別在矩形EFGH的四條邊(不含頂點)上.設∠BAE=θ(弧度),EF的長為y米.
如圖所示,某幼兒園有一個游樂場ABCD,其中AB=50米,BC=40米,由于幼兒園招生規模增大,需將該游樂場擴大成矩形區域EFGH,要求A、B、C、D四個點分別在矩形EFGH的四條邊(不含頂點)上.設∠BAE=θ(弧度),EF的長為y米.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 學生 學科 | A | B | C | D | E |
| 數學成績(x) | 88 | 76 | 73 | 66 | 63 |
| 物理成績(y) | 78 | 65 | 71 | 64 | 61 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com