
【題目】已知拋物線![]() :
:![]() ,過焦點
,過焦點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() ,
,![]() 兩點,且當直線
兩點,且當直線![]() 傾斜角為
傾斜角為![]() 時,與拋物線相交所得弦的長度為8.
時,與拋物線相交所得弦的長度為8.
(1)求拋物線![]() 的方程;
的方程;
(2)若分別過點![]() ,
,![]() 兩點作拋物線
兩點作拋物線![]() 的切線
的切線![]() ,
,![]() ,兩條切線相交于點
,兩條切線相交于點![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() ,判斷四邊形
,判斷四邊形![]() 是否存在外接圓,如果存在,求出外接圓面積的最小值;如果不存在,請說明理由.
是否存在外接圓,如果存在,求出外接圓面積的最小值;如果不存在,請說明理由.
【答案】(1)![]() (2)存在;最小面積為
(2)存在;最小面積為![]()
【解析】
(1)根據題意求出直線![]() 傾斜角為
傾斜角為![]() 時的方程,與拋物線方程聯立,利用根與系數關系和焦半徑公式,求出弦長,即可求出
時的方程,與拋物線方程聯立,利用根與系數關系和焦半徑公式,求出弦長,即可求出![]() ;
;
(2)點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]() ,可得
,可得![]() ,從而有
,從而有![]() ,判斷四邊形
,判斷四邊形![]() 是否存在外接圓,只需判斷是否有
是否存在外接圓,只需判斷是否有![]() ,即
,即![]() 是否垂直,根據切線的幾何意義,求出
是否垂直,根據切線的幾何意義,求出![]() 的斜率,即可得出結論,如果存在外接圓,外接圓的直徑為
的斜率,即可得出結論,如果存在外接圓,外接圓的直徑為![]() ,要使外接圓面積最小,即求
,要使外接圓面積最小,即求![]() 最小,利用根與系數關系和相交弦長公式,即可求解.
最小,利用根與系數關系和相交弦長公式,即可求解.
(1)由題意知![]() ,設點
,設點![]() ,
,![]() ,
,
當直線![]() 傾斜角為
傾斜角為![]() 時,直線
時,直線![]() 的方程為
的方程為![]() ,
,
由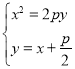 得:
得:![]() ,
,
所以![]() .又由
.又由![]() ,所以
,所以![]() ,
,
所以拋物線的方程為![]() .
.
(2)四邊形![]() 存在外接圓.
存在外接圓.
設直線![]() 方程為
方程為![]() ,
,
代入![]() 中,得
中,得![]() ,則
,則![]() ,
,
且![]() ,
,![]() ,
,
所以![]() ,
,
因為![]() :
:![]() ,即
,即![]() ,所以
,所以![]() .
.
因此,切線![]() 的斜率為
的斜率為![]() ,切線
,切線![]() 的斜率為
的斜率為![]() ,
,
由于![]() ,所以
,所以![]() ,即
,即![]() 是直角三角形,
是直角三角形,
所以![]() 的外接圓的圓心為線段
的外接圓的圓心為線段![]() 的中點,線段
的中點,線段![]() 是圓的直徑,
是圓的直徑,
所以點![]() 一定在
一定在![]() 的外接圓上,即四邊形
的外接圓上,即四邊形![]() 存在外接圓.
存在外接圓.
又因為![]() ,所以當
,所以當![]() 時,線段
時,線段![]() 最短,最短長度為4,
最短,最短長度為4,
此時圓的面積最小,最小面積為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某工廠為提高生產效率,開展技術創新活動,提出了完成某項生產任務的兩種新的生產方式.為比較兩種生產方式的效率,選取![]() 名工人,將他們隨機分成兩組,每組
名工人,將他們隨機分成兩組,每組![]() 人.第一組工人用第一種生產方式,第二組工人用第二種生產方式.根據工人完成生產任務的工作時間(單位:
人.第一組工人用第一種生產方式,第二組工人用第二種生產方式.根據工人完成生產任務的工作時間(單位:![]() )繪制了如圖所示的莖葉圖(莖為十位數,葉為個位數):
)繪制了如圖所示的莖葉圖(莖為十位數,葉為個位數):
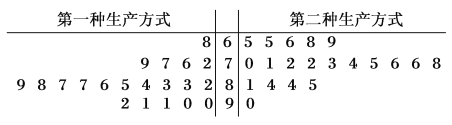
(1)根據莖葉圖,估計兩種生產方式完成任務所需時間至少![]() 分鐘的概率,并對比兩種生產方式所求概率,判斷哪種生產方式的效率更高?
分鐘的概率,并對比兩種生產方式所求概率,判斷哪種生產方式的效率更高?
(2)將完成生產任務所需時間超過![]() 和不超過
和不超過![]() 的工人數填入下面的列聯表:
的工人數填入下面的列聯表:
超過 | 不超過 | |
第一種生產方式 | ||
第二種生產方式 |
(3)根據(2)中的列聯表,能否有![]() 的把握認為兩種生產方式的效率有差異?
的把握認為兩種生產方式的效率有差異?
附: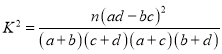
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇跡之一,其中較為著名的是胡夫金字塔.令人吃驚的并不僅僅是胡夫金字塔的雄壯身姿,還有發生在胡夫金字塔上的數字“巧合”.如胡夫金字塔的底部周長如果除以其高度的兩倍,得到的商為3.14159,這就是圓周率較為精確的近似值.金字塔底部形為正方形,整個塔形為正四棱錐,經古代能工巧匠建設完成后,底座邊長大約230米.因年久風化,頂端剝落10米,則胡夫金字塔現高大約為( )
A.128.5米B.132.5米C.136.5米D.110.5米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從編號為1,2,3,4,…,10的10個大小、形狀相同的小球中,任取5個球.如果某兩個球的編號相鄰,則稱這兩個球為一組“好球”.
(1)求任取的5個球中至少有一組“好球”的概率;
(2)在任取的5個球中,記“好球”的組數為X,求隨機變量X的概率分布列和均值E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為![]() (t為參數),若以O為極點,x軸的正半軸為極軸且取相同的單位長度建立極坐標系,曲線C的極坐標方程為
(t為參數),若以O為極點,x軸的正半軸為極軸且取相同的單位長度建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)求曲線C的直角坐標方程及直線l的普通方程;
(2)將所得曲線C向右平移1個單位長度,再將曲線C上的所有點的橫坐標變為原來的2倍,得到曲線![]() ,求曲線
,求曲線![]() 上的點到直線l的距離的最大值.
上的點到直線l的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 的底面是菱形,
的底面是菱形,![]() 底面
底面![]() ,
,![]() 分別是
分別是![]() 的中點,
的中點,![]() ,
,![]() ,
,![]() .
.
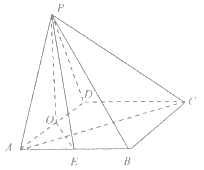
(I)證明:![]() ;
;
(II)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(III)在![]() 邊上是否存在點
邊上是否存在點![]() ,使
,使![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() ,若存在,確定點
,若存在,確定點![]() 位置;若不存在,說明理由.
位置;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com