
 �й����Ľ��cF1��F(xi��n)2��P�ǃ�������һ�����c���t
�й����Ľ��cF1��F(xi��n)2��P�ǃ�������һ�����c���t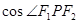 =�� ��
=�� ��A��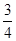 | B��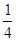 | C��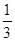 | D�� |
 ÿ��10��犿��������������쾚ϵ�д�
ÿ��10��犿��������������쾚ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}

 .
.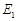 �c
�c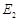 ����ͬ���x����,�^�c
����ͬ���x����,�^�c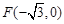 ��ֱ��
��ֱ��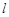 �c
�c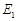 ,
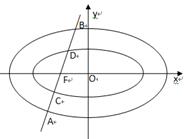
,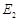 ���ν���A,C,D,B���c(��D).��(d��ng)ֱ��
���ν���A,C,D,B���c(��D).��(d��ng)ֱ��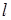 �^
�^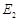 ������c�r, ֱ��
������c�r, ֱ��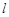 �ăAб�Ǟ�
�ăAб�Ǟ�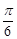 .
.
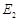 �ķ���;
�ķ���; 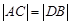 ;
; 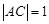 ,��ֱ��
,��ֱ��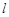 �ķ���.
�ķ���.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
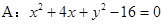 �����c
�����c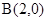 ���cQ�LjAA�ϵĄ��c���cG��BQ�ϣ��cP��QA�ϣ��ҝM��
���cQ�LjAA�ϵĄ��c���cG��BQ�ϣ��cP��QA�ϣ��ҝM��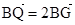 ��
��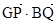 =0��
=0��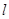 �c����C����M��N���c��ֱ��
�c����C����M��N���c��ֱ��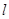 �cy�S����E�c����
�cy�S����E�c����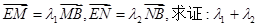 �鶨ֵ��
�鶨ֵ���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
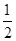 �ęE�AE��һ�����c��AC��x2+y2-4x+2=0�ĈA��.
�ęE�AE��һ�����c��AC��x2+y2-4x+2=0�ĈA��.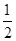 ��ֱ��l1��l2.��(d��ng)ֱ��l1��l2���c�AC���Еr����P������(bi��o).
��ֱ��l1��l2.��(d��ng)ֱ��l1��l2���c�AC���Еr����P������(bi��o).�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}

 ����ͨ���̣�
����ͨ���̣� �ǣ�1��������
�ǣ�1�������� �ϵĄ��c����
�ϵĄ��c����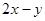 ��ȡֵ������
��ȡֵ�������鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
 ,�ҽ�(j��ng)�^�c
,�ҽ�(j��ng)�^�c ,�^�E�A�����c��ֱ��
,�^�E�A�����c��ֱ�� ���E�A��A��B���c����O(sh��)A��OB����߅��ƽ����߅��OAPB��
���E�A��A��B���c����O(sh��)A��OB����߅��ƽ����߅��OAPB��  ��ʹ����߅��OAPB����Σ������ڣ����ֱ��
��ʹ����߅��OAPB����Σ������ڣ����ֱ�� �ķ��̡��������ڣ��f�����ɡ�
�ķ��̡��������ڣ��f�����ɡ��鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
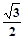 ,���cֱ��x+y+1=0����P��Q���c����OP��OQ����E�A���̡�(O��ԭ�c)��
,���cֱ��x+y+1=0����P��Q���c����OP��OQ����E�A���̡�(O��ԭ�c)���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
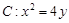 �c�^���Ľ��cF��ֱ��
�c�^���Ľ��cF��ֱ��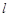 �����ɷ��]����D�ε���e��
�����ɷ��]����D�ε���e��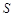 (�Ӱ����)��
(�Ӱ����)��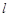 �c���タ
�c���タ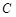 ���ڃ��c
���ڃ��c ,��
,��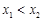 ,ֱ��
,ֱ��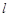 ��б�ʞ�
��б�ʞ�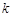 ,ԇ��
,ԇ��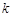 ��ʾ
��ʾ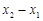 ��
��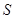 ����Сֵ��
����Сֵ��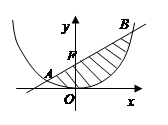
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
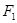 ��
��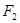 �ǙE�A
�ǙE�A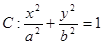 ��
�� ��
��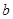 ��0���ăɂ����c��
��0���ăɂ����c��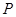 ��E�A
��E�A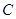 ��һ�c����
��һ�c����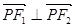 .��
.��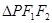 ����e��9���t
����e��9���t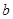 ="____________."
="____________." �鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com