
分析 先將關于x的方程ax=x,再畫出a>1時函數y=ax,y=a的圖象,根據圖象求解函數的導數求出最小值大于0,利用對數運算法則化簡求解即可.
解答 解:據題意,關于x的方程ax=x無實根.
函數y=ax,的圖象與直線y=x沒有的交點.
a>1時:如圖: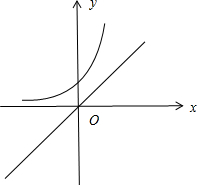
方程ax=x,即ax-x=0,令y=ax-x
函數y′=axlna-1,函數的極值點為:x=$lo{g}_{a}ln{a}^{-1}$,并且是最小值點,必須${a}^{lo{g}_{a}ln{a}^{-1}}-lo{g}_{a}ln{a}^{-1}>0$,可得:$ln{a}^{-1}>\frac{lnln{a}^{-1}}{lna}$,即1>lnlna-1,任意x使得lna-1<e,a-1<ee,∴a>${e}^{\frac{1}{e}}$.
則實數a的取值范圍為 (${e}^{\frac{1}{e}}$,+∞)
故答案為:$({e^{\frac{1}{e}}},+∞)$.
點評 本題主要考查函數的導數的應用,函數的最值以及極值的求法,對數的運算法則的應用,考查數形結合,轉化思想的應用,考查計算能力.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | (-∞,4] | B. | (-∞,2] | C. | [4,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
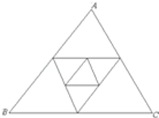 如圖,已知△ABC周長為2,連接△ABC三邊的中點構成第二個三角形,再連接第二個對角線三邊中點構成第三個三角形,依此類推,第2003個三角形周長為( )
如圖,已知△ABC周長為2,連接△ABC三邊的中點構成第二個三角形,再連接第二個對角線三邊中點構成第三個三角形,依此類推,第2003個三角形周長為( )| A. | $\frac{1}{2002}$ | B. | $\frac{1}{2001}$ | C. | $\frac{1}{{2}^{2002}}$ | D. | 2${\;}^{\frac{1}{2001}}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
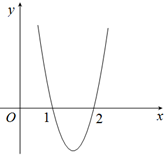 已知函數f(x)=2x3+bx2+cx,其導函數y=f′(x)的圖象(如圖所示)經過點(1,0),(2,0).
已知函數f(x)=2x3+bx2+cx,其導函數y=f′(x)的圖象(如圖所示)經過點(1,0),(2,0).查看答案和解析>>
科目:高中數學 來源: 題型:填空題

查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 原始社會時期,人們通過在繩子上打結來計算數量,即“結繩計數”,當時有位父親,為了準確記錄孩子的成長天數,在粗細不同的繩子上打結,由細到粗,滿七進一,如圖所示,孩子已經出生468天.
原始社會時期,人們通過在繩子上打結來計算數量,即“結繩計數”,當時有位父親,為了準確記錄孩子的成長天數,在粗細不同的繩子上打結,由細到粗,滿七進一,如圖所示,孩子已經出生468天.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2017屆安徽合肥一中高三上學期月考一數學(文)試卷(解析版) 題型:選擇題
如圖所示,點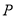 從點
從點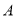 處出發,按逆時針方向沿邊長為
處出發,按逆時針方向沿邊長為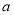 的正三角形
的正三角形 運動一周,
運動一周,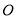 為
為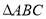 的中心,設點
的中心,設點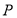 走過的路程為
走過的路程為 ,
,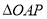 的面積為
的面積為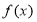 (當
(當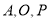 三點共線時,記面積為0),則函數
三點共線時,記面積為0),則函數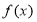 的圖象大致為( )
的圖象大致為( )
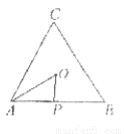
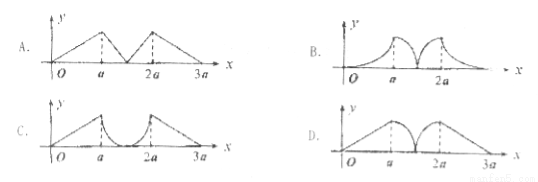
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com