
【題目】已知函數(shù)![]() .
.
(1)當![]() 時,求證:若
時,求證:若![]() ,則
,則![]() ;
;
(2)當![]() 時,試討論函數(shù)
時,試討論函數(shù)![]() 的零點個數(shù).
的零點個數(shù).
【答案】(Ⅰ)證明見解析;(Ⅱ)當![]() 時,函數(shù)
時,函數(shù)![]() 有且僅有一個零點,當
有且僅有一個零點,當![]() 時,函數(shù)
時,函數(shù)![]() 有兩個零點.
有兩個零點.
【解析】
試題(1)函數(shù)求導(dǎo)![]() ,再求導(dǎo)得
,再求導(dǎo)得![]() 恒成立,又因為
恒成立,又因為![]() 恒成立;
恒成立;
(2)由(1)可知,當x≤0時,f″(x)≤0,可得 對x∈R,f′(x)≥0,即ex≥x+1,分類討論當x≥-1時,當x<-1時,函數(shù)y=f(x)的零點個數(shù)即可得解;
當x<-1時,再分0≤m≤1和m<0兩種情況進行討論,由函數(shù)零點定理進行判斷即可得到答案.
試題解析:,所以
(1)當![]() 時,
時,![]() ,則
,則![]() ,令
,令![]() ,則
,則![]() ,當
,當![]() 時,
時,![]() ,即
,即![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 上為增函數(shù),即當
上為增函數(shù),即當![]() 時,
時,![]() ,所以當
,所以當![]() 時,
時,![]() 恒成立,所以函數(shù)
恒成立,所以函數(shù)![]() 在
在![]() 上為增函數(shù),又因為
上為增函數(shù),又因為![]() ,所以當
,所以當![]() 時,對
時,對![]() 恒成立.
恒成立.
(2)由(1)知,當![]()
![]() ,所以
,所以![]() ,所以函數(shù)
,所以函數(shù)![]() 的減區(qū)間為
的減區(qū)間為![]() ,增函數(shù)為
,增函數(shù)為![]() .所以
.所以![]() ,所以對
,所以對![]()
![]() ,
,![]() ,即
,即![]() .
.
①當![]() 時,
時,![]() ,又
,又![]() ,
,![]() ,即
,即![]() ,所以當
,所以當![]() 時,函數(shù)
時,函數(shù)![]() 為增函數(shù),又
為增函數(shù),又![]() ,所以當
,所以當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上有且僅有一個零點,且為
上有且僅有一個零點,且為![]() .
.
②當![]() 時,(ⅰ)當
時,(ⅰ)當![]() 時,
時,![]() ,所以
,所以![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 上遞增,所以
上遞增,所以![]() ,且
,且![]() ,故
,故![]() 時,函數(shù)
時,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上無零點.
上無零點.
(ⅱ)當![]() 時,
時, ![]() ,令
,令![]() ,則
,則![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,![]() ,當
,當![]() 時,
時,![]() ,又曲線
,又曲線![]() 在區(qū)間
在區(qū)間![]() 上不間斷,所以
上不間斷,所以![]() ,使
,使![]() ,故當
,故當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 的減區(qū)間為
的減區(qū)間為![]() ,增區(qū)間為
,增區(qū)間為![]() ,又
,又![]() ,所以對
,所以對![]() ,又當
,又當![]() 時,
時,![]() ,又
,又![]() ,曲線
,曲線![]() 在區(qū)間
在區(qū)間![]() 上不間斷.所以
上不間斷.所以![]() ,且唯一實數(shù)
,且唯一實數(shù)![]() ,使得
,使得![]() ,綜上,當
,綜上,當![]() 時,函數(shù)
時,函數(shù)![]() 有且僅有一個零點;當
有且僅有一個零點;當![]() 時,函數(shù)
時,函數(shù)![]() 有個兩零點.
有個兩零點.


 波波熊暑假作業(yè)江西人民出版社系列答案
波波熊暑假作業(yè)江西人民出版社系列答案 學(xué)而優(yōu)暑期銜接南京大學(xué)出版社系列答案
學(xué)而優(yōu)暑期銜接南京大學(xué)出版社系列答案 Happy holiday歡樂假期暑假作業(yè)廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業(yè)廣東人民出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,PA⊥平面ABCD,四邊形ABCD是矩形,![]() ,
,![]() ,點F為PB中點,點E在邊BC上移動.
,點F為PB中點,點E在邊BC上移動.
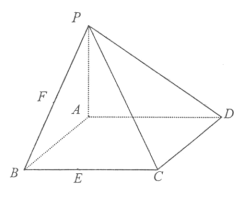
(Ⅰ)求證:PD∥平面AFC;
(Ⅱ)若![]() ,求證:
,求證:![]() ;
;
(Ⅲ)若二面角![]() 的大小為60°,則CE為何值時,三棱錐
的大小為60°,則CE為何值時,三棱錐![]() 的體積為
的體積為![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的一個頂點為
的一個頂點為![]() ,離心率
,離心率![]() ,直線
,直線![]() 交橢圓于
交橢圓于![]() 、
、![]() 兩點.
兩點.
(1)若直線![]() 的方程為
的方程為![]() ,求弦
,求弦![]() 的長;
的長;
(2)如果![]() 的重心恰好為橢圓的右焦點
的重心恰好為橢圓的右焦點![]() ,求直線
,求直線![]() 方程的一般式.
方程的一般式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的中心在坐標原點,焦點在
的中心在坐標原點,焦點在![]() 軸上,左頂點為
軸上,左頂點為![]() ,左焦點為
,左焦點為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,直線
上,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,直線
兩點,直線![]() ,
, ![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,
, ![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)以![]() 為直徑的圓是否經(jīng)過定點?若經(jīng)過,求出定點的坐標;若不經(jīng)過,請說明理由.
為直徑的圓是否經(jīng)過定點?若經(jīng)過,求出定點的坐標;若不經(jīng)過,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】自2016年1月1日起,我國全面二孩政策正式實施,這次人口與生育政策的歷史性調(diào)整,使得“要不要再生一個”,“生二孩能休多久產(chǎn)假”等問題成為千千萬萬個家庭在生育決策上避不開的話題.為了解針對產(chǎn)假的不同安排方案形成的生育意愿,某調(diào)查機構(gòu)隨機抽取了200戶有生育二胎能力的適齡家庭進行問卷調(diào)查,得到如下數(shù)據(jù):
產(chǎn)假安排(單位:周) | 14 | 15 | 16 | 17 | 18 |
有生育意愿家庭數(shù) | 4 | 8 | 16 | 20 | 26 |
(1)若用表中數(shù)據(jù)所得的頻率代替概率,面對產(chǎn)假為14周與16周,估計某家庭有生育意愿的概率分別為多少?
(2)假設(shè)從5種不同安排方案中,隨機抽取2種不同安排分別作為備選方案,然后由單位根據(jù)單位情況自主選擇.
①求兩種安排方案休假周數(shù)和不低于32周的概率;
②如果用![]() 表示兩種方案休假周數(shù)之和.求隨機變量
表示兩種方案休假周數(shù)之和.求隨機變量![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
, ![]() ,其中
,其中![]() R,
R, ![]() …為自然對數(shù)的底數(shù).
…為自然對數(shù)的底數(shù).
(Ⅰ)當![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(Ⅱ)求證: ![]() (參考數(shù)據(jù):
(參考數(shù)據(jù): ![]() ).
).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C:![]() 及點P(0,1),過點P的直線與圓交于A、B兩點.
及點P(0,1),過點P的直線與圓交于A、B兩點.
(1)若弦長![]() 求直線AB的斜率;
求直線AB的斜率;
(2)求△ABC面積的最大值,及此時弦長![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】雙曲線![]() :
:![]() 的左右頂點分別為
的左右頂點分別為![]() ,
,![]() ,動直線
,動直線![]() 垂直
垂直![]() 的實軸,且交
的實軸,且交![]() 于不同的兩點
于不同的兩點![]() ,直線
,直線![]() 與直線
與直線![]() 的交點為
的交點為![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 作
作![]() 的兩條互相垂直的弦
的兩條互相垂直的弦![]() ,
,![]() ,證明:過兩弦
,證明:過兩弦![]() ,
,![]() 中點的直線恒過定點.
中點的直線恒過定點.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com